Question Number 118347 by bramlexs22 last updated on 17/Oct/20
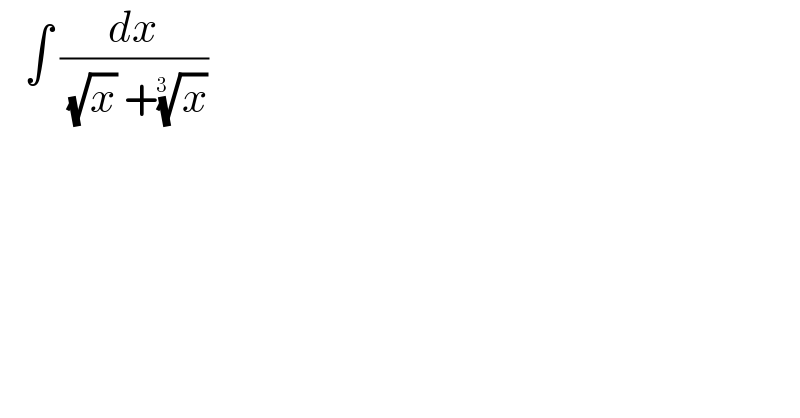
$$\:\:\:\int\:\frac{{dx}}{\:\sqrt{{x}}\:+\sqrt[{\mathrm{3}\:}]{{x}}}\: \\ $$
Answered by benjo_mathlover last updated on 17/Oct/20
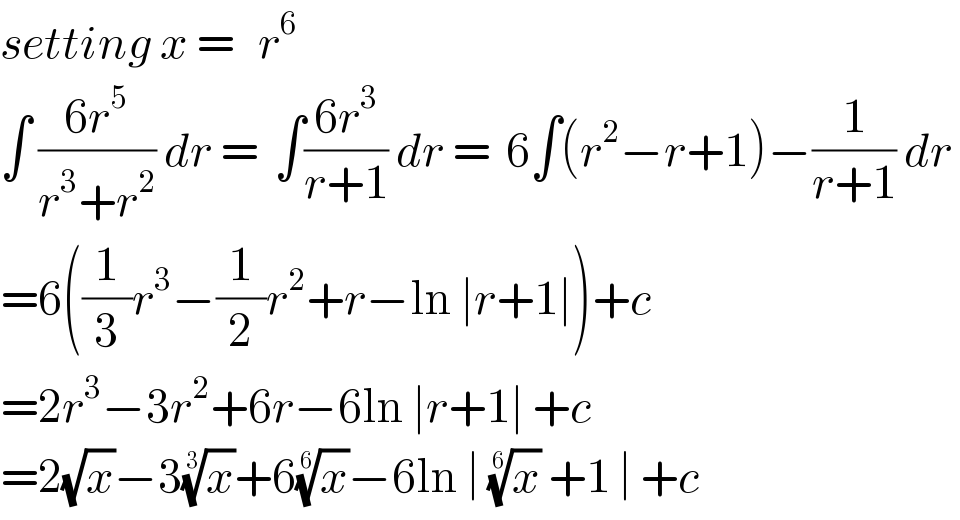
$${setting}\:{x}\:=\:\:\:{r}^{\mathrm{6}} \\ $$$$\int\:\frac{\mathrm{6}{r}^{\mathrm{5}} }{{r}^{\mathrm{3}} +{r}^{\mathrm{2}} }\:{dr}\:=\:\:\int\frac{\mathrm{6}{r}^{\mathrm{3}} }{{r}+\mathrm{1}}\:{dr}\:=\:\:\mathrm{6}\int\left({r}^{\mathrm{2}} −{r}+\mathrm{1}\right)−\frac{\mathrm{1}}{{r}+\mathrm{1}}\:{dr}\: \\ $$$$=\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{3}}{r}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} +{r}−\mathrm{ln}\:\mid{r}+\mathrm{1}\mid\right)+{c} \\ $$$$=\mathrm{2}{r}^{\mathrm{3}} −\mathrm{3}{r}^{\mathrm{2}} +\mathrm{6}{r}−\mathrm{6ln}\:\mid{r}+\mathrm{1}\mid\:+{c} \\ $$$$=\mathrm{2}\sqrt{{x}}−\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}+\mathrm{6}\sqrt[{\mathrm{6}}]{{x}}−\mathrm{6ln}\:\mid\:\sqrt[{\mathrm{6}}]{{x}}\:+\mathrm{1}\:\mid\:+{c} \\ $$
