Question Number 103511 by bemath last updated on 15/Jul/20

$$\int\:\frac{{dx}}{\:\sqrt{{x}}\:\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)}\:=\_\_ \\ $$$$\left({a}\right)\:−\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}}{\mathrm{18}\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)^{\mathrm{9}} }\:+\:{c}\: \\ $$$$\left({b}\right)\:\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}}{\mathrm{18}\left(\sqrt[{\mathrm{4}}]{{x}}+\mathrm{1}\right)^{\mathrm{9}} }\:+{c} \\ $$$$\left({c}\right)\:−\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}\:−\mathrm{1}}{\mathrm{18}\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)^{\mathrm{9}} }\:+{c} \\ $$$$\left({d}\right)\:\frac{\mathrm{9}\:\sqrt[{\mathrm{4}}]{{x}}+\mathrm{1}}{\mathrm{8}\left(\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}\right)^{\mathrm{9}} }\:+\:{c} \\ $$
Commented by bobhans last updated on 15/Jul/20
$${nothing}\:{answer} \\ $$
Answered by bramlex last updated on 15/Jul/20
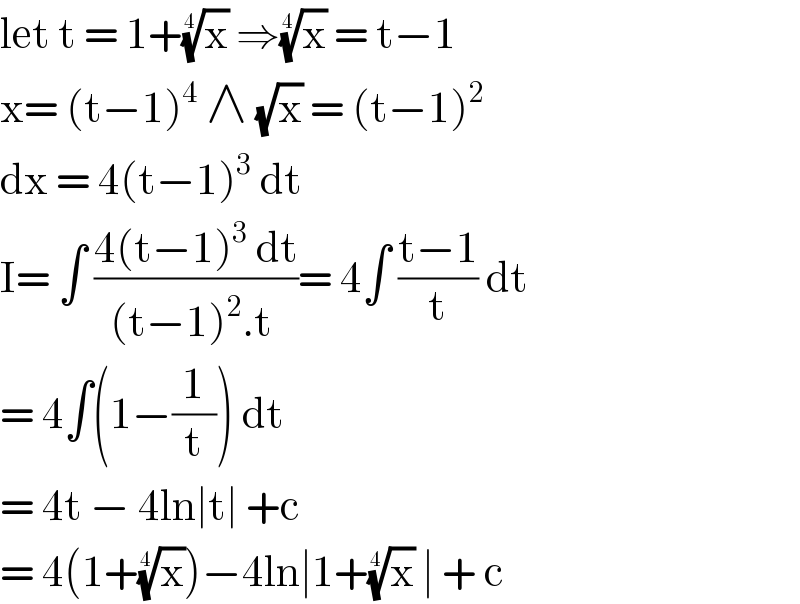
$$\mathrm{let}\:\mathrm{t}\:=\:\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\Rightarrow\sqrt[{\mathrm{4}}]{\mathrm{x}}\:=\:\mathrm{t}−\mathrm{1} \\ $$$$\mathrm{x}=\:\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} \:\wedge\:\sqrt{\mathrm{x}}\:=\:\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{dx}\:=\:\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{3}} \:\mathrm{dt}\: \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{4}\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{3}} \:\mathrm{dt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} .\mathrm{t}\:}=\:\mathrm{4}\int\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}}\:\mathrm{dt} \\ $$$$=\:\mathrm{4}\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}}\right)\:\mathrm{dt}\: \\ $$$$=\:\mathrm{4t}\:−\:\mathrm{4ln}\mid\mathrm{t}\mid\:+\mathrm{c}\: \\ $$$$=\:\mathrm{4}\left(\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}}\right)−\mathrm{4ln}\mid\mathrm{1}+\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\mid\:+\:\mathrm{c}\: \\ $$
