Question Number 85637 by jagoll last updated on 23/Mar/20
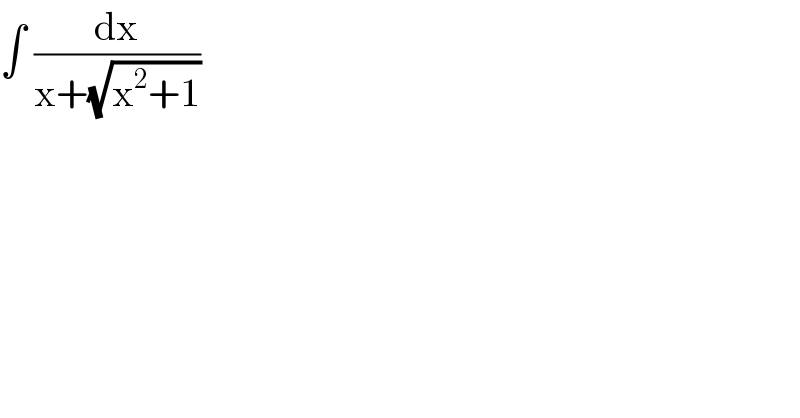
$$\int\:\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\: \\ $$
Commented by abdomathmax last updated on 23/Mar/20
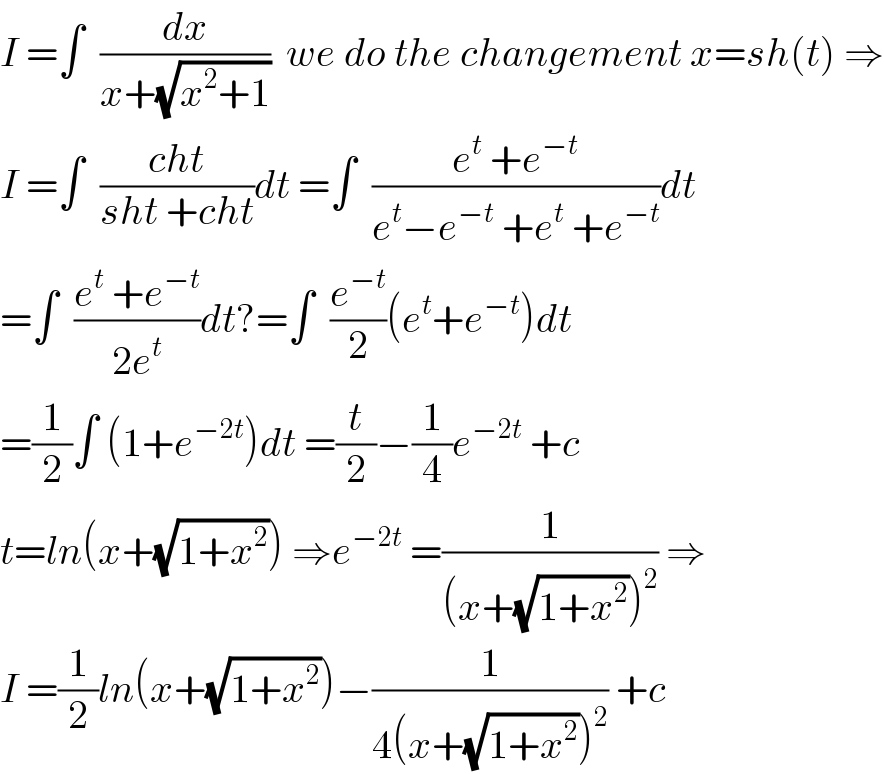
$${I}\:=\int\:\:\frac{{dx}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\:{we}\:{do}\:{the}\:{changement}\:{x}={sh}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\int\:\:\frac{{cht}}{{sht}\:+{cht}}{dt}\:=\int\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{{e}^{{t}} −{e}^{−{t}} \:+{e}^{{t}} \:+{e}^{−{t}} }{dt} \\ $$$$=\int\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}{e}^{{t}} }{dt}?=\int\:\:\frac{{e}^{−{t}} }{\mathrm{2}}\left({e}^{{t}} +{e}^{−{t}} \right){dt}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{1}+{e}^{−\mathrm{2}{t}} \right){dt}\:=\frac{{t}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\mathrm{2}{t}} \:+{c} \\ $$$${t}={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:\Rightarrow{e}^{−\mathrm{2}{t}} \:=\frac{\mathrm{1}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{\mathrm{4}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:+{c}\: \\ $$
Commented by john santu last updated on 23/Mar/20
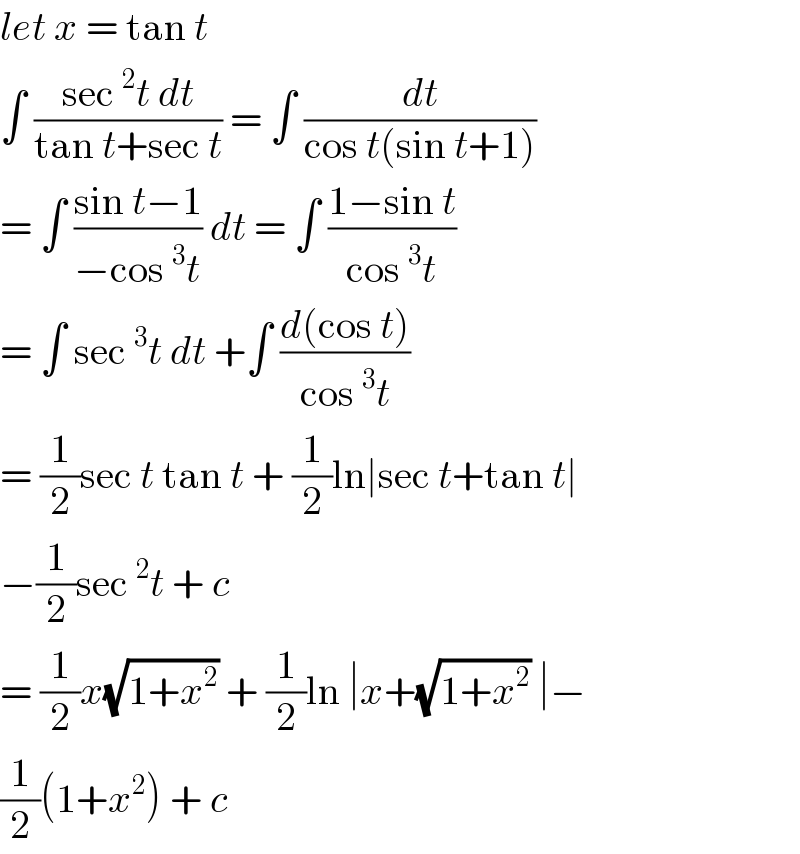
$${let}\:{x}\:=\:\mathrm{tan}\:{t} \\ $$$$\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} {t}\:{dt}}{\mathrm{tan}\:{t}+\mathrm{sec}\:{t}}\:=\:\int\:\frac{{dt}}{\mathrm{cos}\:{t}\left(\mathrm{sin}\:{t}+\mathrm{1}\right)} \\ $$$$=\:\int\:\frac{\mathrm{sin}\:{t}−\mathrm{1}}{−\mathrm{cos}\:^{\mathrm{3}} {t}}\:{dt}\:=\:\int\:\frac{\mathrm{1}−\mathrm{sin}\:{t}}{\mathrm{cos}\:^{\mathrm{3}} {t}} \\ $$$$=\:\int\:\mathrm{sec}\:^{\mathrm{3}} {t}\:{dt}\:+\int\:\frac{{d}\left(\mathrm{cos}\:{t}\right)}{\mathrm{cos}\:^{\mathrm{3}} {t}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:{t}\:\mathrm{tan}\:{t}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{sec}\:{t}+\mathrm{tan}\:{t}\mid\: \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} {t}\:+\:{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mid− \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:+\:{c} \\ $$
Answered by MJS last updated on 23/Mar/20
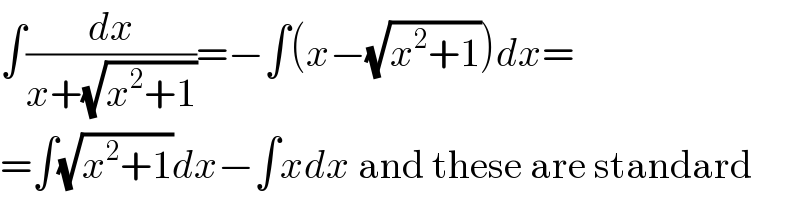
$$\int\frac{{dx}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}=−\int\left({x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx}= \\ $$$$=\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\int{xdx}\:\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{standard} \\ $$
Commented by john santu last updated on 24/Mar/20
$${hahaha}..{standard}\:{sir} \\ $$$$ \\ $$
