Question Number 157442 by bobhans last updated on 23/Oct/21
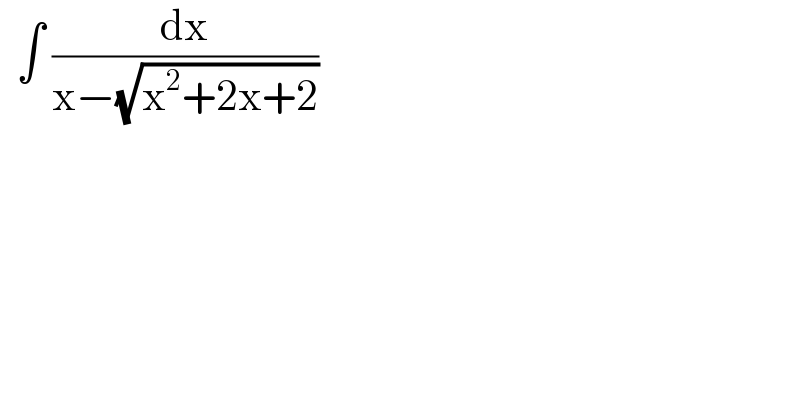
$$\:\:\int\:\frac{\mathrm{dx}}{\mathrm{x}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}}\: \\ $$
Answered by MJS_new last updated on 23/Oct/21
![∫(dx/(x−(√(x^2 +2x+2))))= [t=x+1+(√(x^2 +2x+2)) → dx=((√(x^2 +2x+2))/(x+1+(√(x^2 +2x+2))))dt] =−(1/2)∫((t^2 +1)/(t(t+1)))dt=∫((1/(t+1))−(1/(2t))−(1/2))dt= =ln (t+1) −(1/2)ln t −(1/2)t= =(1/2)(ln (((t+1)^2 )/t) −t)= =(1/2)(ln (1+(√(x^2 +2x+2))) −x−(√(x^2 +2x+2)))+C](https://www.tinkutara.com/question/Q157447.png)
$$\int\frac{{dx}}{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}{{x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}{dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}\left({t}+\mathrm{1}\right)}{dt}=\int\left(\frac{\mathrm{1}}{{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{t}}−\frac{\mathrm{1}}{\mathrm{2}}\right){dt}= \\ $$$$=\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{t}\:−\frac{\mathrm{1}}{\mathrm{2}}{t}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}}\:−{t}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:\left(\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}\right)\:−{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}\right)+{C} \\ $$
Answered by cortano last updated on 23/Oct/21

$$\frac{\mathrm{1}}{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}\:=\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}{−\mathrm{2}{x}−\mathrm{2}} \\ $$$${I}=−\int\frac{{x}}{\mathrm{2}{x}+\mathrm{2}}\:{dx}−\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}}}{\mathrm{2}{x}+\mathrm{2}}\:{dx} \\ $$$${I}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{x}+\mathrm{1}−\mathrm{1}}{{x}+\mathrm{1}}\:{dx}=−\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{ln}\:\mid{x}+\mathrm{1}\mid+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}}{{x}+\mathrm{1}}\:{dx} \\ $$$${x}+\mathrm{1}=\mathrm{tan}\:{u} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{sec}\:{u}}{\mathrm{tan}\:{u}}\:\mathrm{sec}\:^{\mathrm{2}} \:{du} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\:{csc}\:{x}\:\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx} \\ $$$${IBP}\:\Rightarrow\begin{cases}{{u}={csc}\:{x}\Rightarrow{du}=−{csc}\:{x}\:\mathrm{cot}\:{x}\:{dx}}\\{{v}=\mathrm{tan}\:{x}}\end{cases} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\left\{{csc}\:{x}\:\mathrm{tan}\:{x}+\int\:{csc}\:{x}\:{dx}\:\right\} \\ $$$${I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}{csc}\:{x}\:\mathrm{tan}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{csc}\:{x}−\mathrm{cot}\:{x}\mid\:+{c}_{\mathrm{2}} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$
