Question Number 35456 by math1967 last updated on 19/May/18

$$\int\frac{{dx}}{{x}\left({x}^{\mathrm{2018}} +\mathrm{1}\right)} \\ $$
Answered by ajfour last updated on 19/May/18
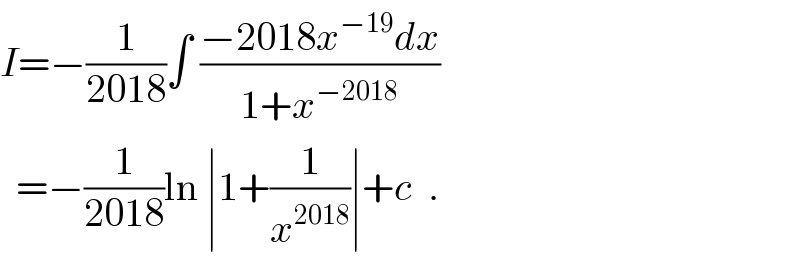
$${I}=−\frac{\mathrm{1}}{\mathrm{2018}}\int\:\frac{−\mathrm{2018}{x}^{−\mathrm{19}} {dx}}{\mathrm{1}+{x}^{−\mathrm{2018}} } \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2018}}\mathrm{ln}\:\mid\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2018}} }\mid+{c}\:\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/May/18
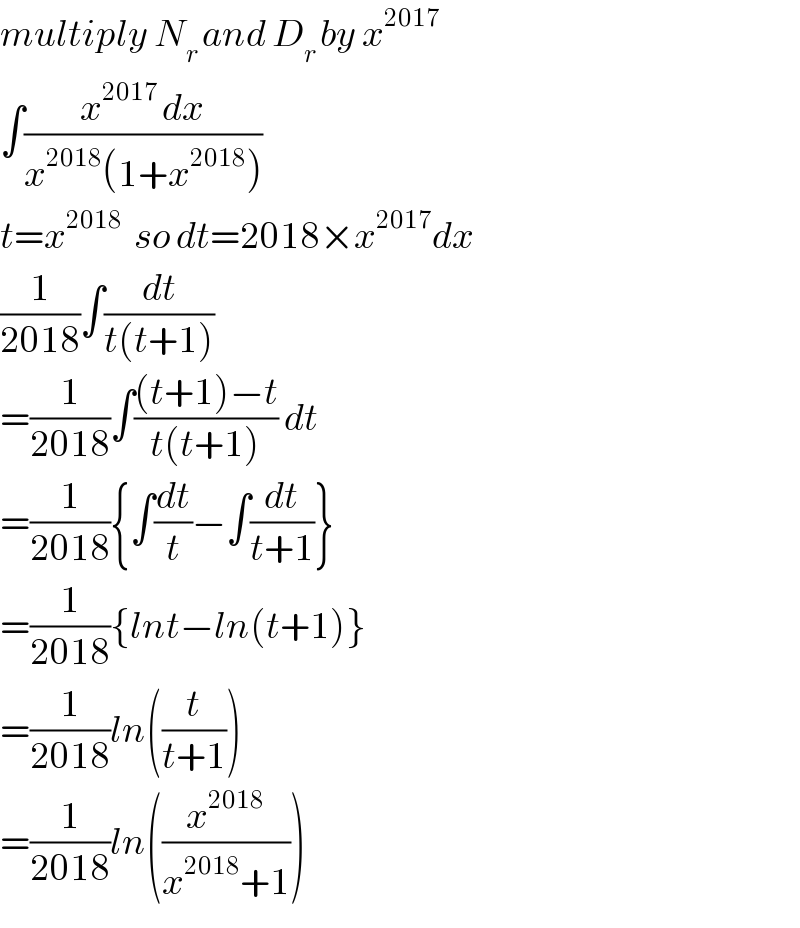
$${multiply}\:{N}_{{r}\:} {and}\:{D}_{{r}\:} {by}\:{x}^{\mathrm{2017}} \\ $$$$\int\frac{{x}^{\mathrm{2017}\:} {dx}}{{x}^{\mathrm{2018}} \left(\mathrm{1}+{x}^{\mathrm{2018}} \right)} \\ $$$${t}={x}^{\mathrm{2018}\:\:\:} {so}\:{dt}=\mathrm{2018}×{x}^{\mathrm{2017}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2018}}\int\frac{{dt}}{{t}\left({t}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2018}}\int\frac{\left({t}+\mathrm{1}\right)−{t}}{{t}\left({t}+\mathrm{1}\right)}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2018}}\left\{\int\frac{{dt}}{{t}}−\int\frac{{dt}}{{t}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2018}}\left\{{lnt}−{ln}\left({t}+\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2018}}{ln}\left(\frac{{t}}{{t}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2018}}{ln}\left(\frac{{x}^{\mathrm{2018}} }{{x}^{\mathrm{2018}} +\mathrm{1}}\right) \\ $$
