Menu Close

dx-x-x-x-1-

Tinku Tara 0 Comments
Pin




Question Number 157309 by cortano last updated on 22/Oct/21
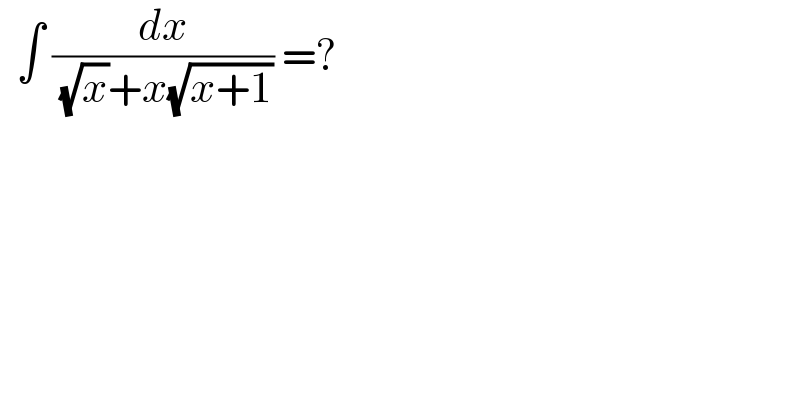
∫ (dx/( (√x)+x(√(x+1)))) =?
$$\:\:\int\:\frac{{dx}}{\:\sqrt{{x}}+{x}\sqrt{{x}+\mathrm{1}}}\:=? \\ $$
Answered by MJS_new last updated on 22/Oct/21
∫(dx/( (√x)+x(√(x+1))))= =∫((√(x+1))/(x^2 +x−1))dx−∫(dx/((x^2 +x−1)(√x))) ∫((√(x+1))/(x^2 +x−1))dx= [t=(√(x+1)) → dx=2(√(x+1))dt] =2∫(t^2 /(t^4 −t^2 +1))dt ... −∫(dx/((x^2 +x−1)(√x)))= [u=(√x) → dx=2(√x)du] =−2∫(du/(u^4 +u^2 −1)) ...
$$\int\frac{{dx}}{\:\sqrt{{x}}+{x}\sqrt{{x}+\mathrm{1}}}= \\ $$$$=\int\frac{\sqrt{{x}+\mathrm{1}}}{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{dx}−\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)\sqrt{{x}}} \\ $$$$ \\ $$$$\int\frac{\sqrt{{x}+\mathrm{1}}}{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}+\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}+\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} −{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$… \\ $$$$ \\ $$$$−\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}−\mathrm{1}\right)\sqrt{{x}}}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{du}\right] \\ $$$$=−\mathrm{2}\int\frac{{du}}{{u}^{\mathrm{4}} +{u}^{\mathrm{2}} −\mathrm{1}} \\ $$$$… \\ $$
Commented by lyubita last updated on 22/Oct/21
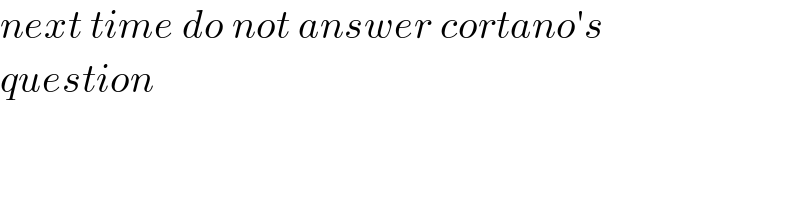
next time do not answer cortano′s question
$${next}\:{time}\:{do}\:{not}\:{answer}\:{cortano}'{s} \\ $$$${question} \\ $$
Commented by cortano last updated on 22/Oct/21
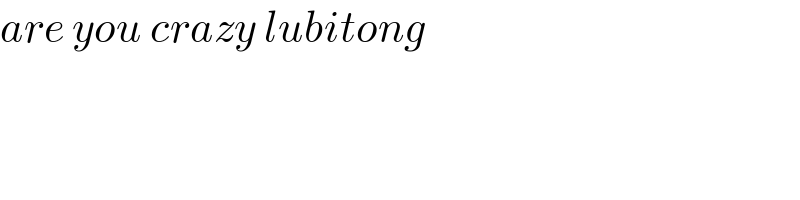
are you crazy lubitong
$${are}\:{you}\:{crazy}\:{lubitong} \\ $$
Answered by MJS_new last updated on 22/Oct/21
∫(dx/( (√x)+x(√(x+1))))= [t=(√x)+(√(x+1)) → dx=((2(√x)(√(x+1)))/( (√x)+(√(x+1))))dt] =4∫((t^2 +1)/(t^4 +4t^2 −1))dt ...
$$\int\frac{{dx}}{\:\sqrt{{x}}+{x}\sqrt{{x}+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{{x}}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}}{dt}\right] \\ $$$$=\mathrm{4}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$… \\ $$
Commented by cortano last updated on 22/Oct/21
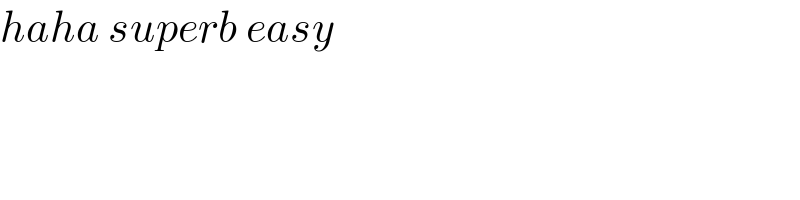
haha superb easy
$${haha}\:{superb}\:{easy} \\ $$
Commented by yeti123 last updated on 22/Oct/21
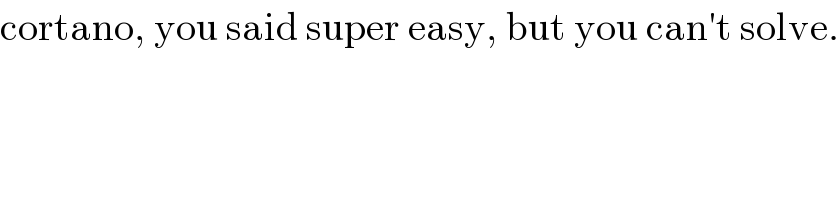
cortano, you said super easy, but you can′t solve.
$$\mathrm{cortano},\:\mathrm{you}\:\mathrm{said}\:\mathrm{super}\:\mathrm{easy},\:\mathrm{but}\:\mathrm{you}\:\mathrm{can}'\mathrm{t}\:\mathrm{solve}. \\ $$
Commented by cortano last updated on 22/Oct/21
hey how do you know i can't finish it? are you God?
Commented by MJS_new last updated on 22/Oct/21
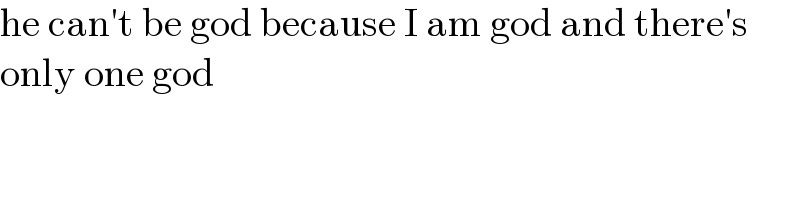
he can′t be god because I am god and there′s only one god
$$\mathrm{he}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{god}\:\mathrm{because}\:\mathrm{I}\:\mathrm{am}\:\mathrm{god}\:\mathrm{and}\:\mathrm{there}'\mathrm{s} \\ $$$$\mathrm{only}\:\mathrm{one}\:\mathrm{god} \\ $$
Commented by ajfour last updated on 22/Oct/21
why did u have to divulge that so soon, we had planned to keep him foolinround a little longer..
$${why}\:{did}\:{u}\:{have}\:{to}\:{divulge}\:{that} \\ $$$${so}\:{soon},\:{we}\:{had}\:{planned}\:{to} \\ $$$${keep}\:{him}\:{foolinround}\:{a}\:{little} \\ $$$${longer}.. \\ $$
Commented by MJS_new last updated on 22/Oct/21
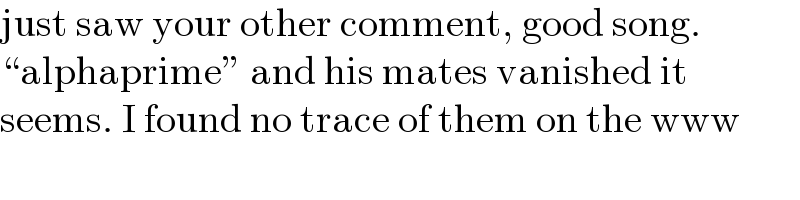
just saw your other comment, good song. “alphaprime” and his mates vanished it seems. I found no trace of them on the www
$$\mathrm{just}\:\mathrm{saw}\:\mathrm{your}\:\mathrm{other}\:\mathrm{comment},\:\mathrm{good}\:\mathrm{song}. \\ $$$$“\mathrm{alphaprime}''\:\mathrm{and}\:\mathrm{his}\:\mathrm{mates}\:\mathrm{vanished}\:\mathrm{it} \\ $$$$\mathrm{seems}.\:\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{trace}\:\mathrm{of}\:\mathrm{them}\:\mathrm{on}\:\mathrm{the}\:\mathrm{www} \\ $$
Commented by ajfour last updated on 22/Oct/21
please check alphaprime.slack.com
Commented by cortano last updated on 22/Oct/21
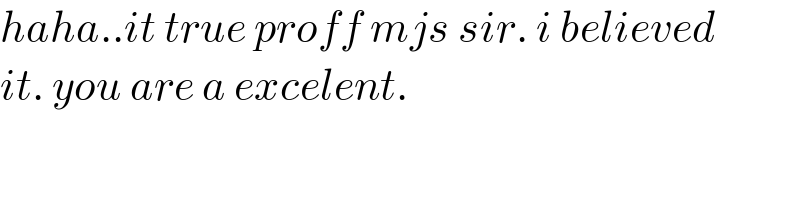
haha..it true proff mjs sir. i believed it. you are a excelent.
$${haha}..{it}\:{true}\:{proff}\:{mjs}\:{sir}.\:{i}\:{believed} \\ $$$${it}.\:{you}\:{are}\:{a}\:{excelent}. \\ $$
Commented by talminator2856791 last updated on 22/Oct/21
it sound like you all know each other personally.
$$\:\mathrm{it}\:\mathrm{sound}\:\mathrm{like}\:\mathrm{you}\:\mathrm{all}\:\mathrm{know}\:\mathrm{each}\:\mathrm{other}\:\:\: \\ $$$$\:\mathrm{personally}. \\ $$
Commented by cortano last updated on 23/Oct/21
I=4∫ ((t^2 +1)/((t^2 +2)^2 −5)) dt I=4∫ ((t^2 +1)/((t^2 +2+(√5))(t^2 +2−(√5)))) dt I=4∫ {(((1/(10))((√5)+5))/(t^2 +((√5)+2)))+(((1/(10))((√5)−5))/(t^2 −((√5)−2)))}dt I=((2((√5)+5))/(5(√((√5)+2)))) arctan ((t/( (√((√5)−2)))))−((2((√5)−5))/(5(√((√5)−2))))tanh^(−1) ((t/( (√((√5)−2)))))+C where t=(√(x+1))+(√x)
$${I}=\mathrm{4}\int\:\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}}\:{dt}\: \\ $$$${I}=\mathrm{4}\int\:\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{2}+\sqrt{\mathrm{5}}\right)\left({t}^{\mathrm{2}} +\mathrm{2}−\sqrt{\mathrm{5}}\right)}\:{dt} \\ $$$${I}=\mathrm{4}\int\:\left\{\frac{\frac{\mathrm{1}}{\mathrm{10}}\left(\sqrt{\mathrm{5}}+\mathrm{5}\right)}{{t}^{\mathrm{2}} +\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)}+\frac{\frac{\mathrm{1}}{\mathrm{10}}\left(\sqrt{\mathrm{5}}−\mathrm{5}\right)}{{t}^{\mathrm{2}} −\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}\right\}{dt} \\ $$$${I}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{5}\right)}{\mathrm{5}\sqrt{\sqrt{\mathrm{5}}+\mathrm{2}}}\:\mathrm{arctan}\:\left(\frac{{t}}{\:\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}\right)−\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{5}\right)}{\mathrm{5}\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}\mathrm{tanh}\:^{−\mathrm{1}} \left(\frac{{t}}{\:\sqrt{\sqrt{\mathrm{5}}−\mathrm{2}}}\right)+{C} \\ $$$${where}\:{t}=\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}\: \\ $$
Answered by ajfour last updated on 22/Oct/21
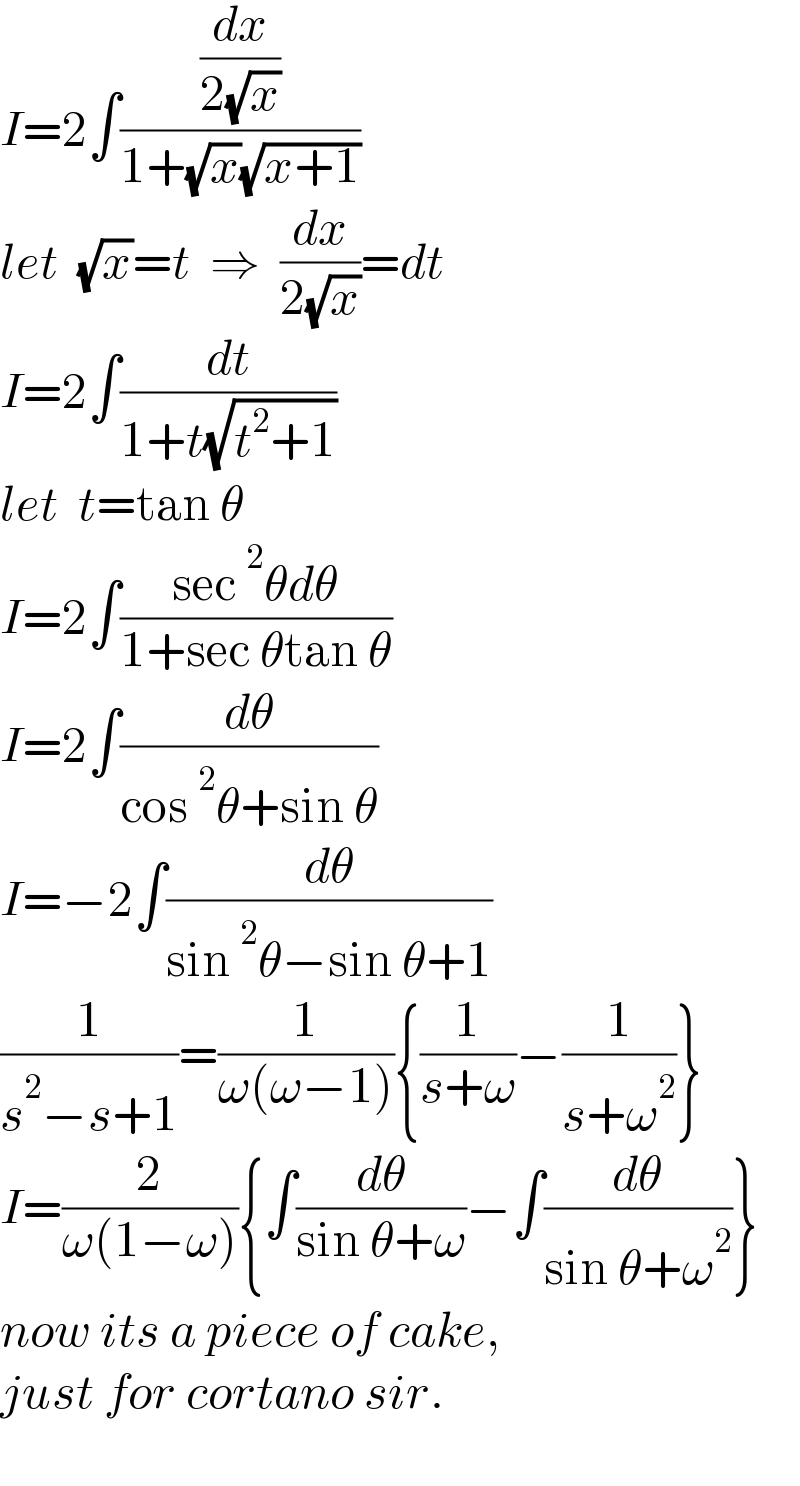
I=2∫((dx/(2(√x)))/(1+(√x)(√(x+1)))) let (√x)=t ⇒ (dx/(2(√x)))=dt I=2∫(dt/(1+t(√(t^2 +1)))) let t=tan θ I=2∫((sec^2 θdθ)/(1+sec θtan θ)) I=2∫(dθ/(cos^2 θ+sin θ)) I=−2∫(dθ/(sin^2 θ−sin θ+1)) (1/(s^2 −s+1))=(1/(ω(ω−1))){(1/(s+ω))−(1/(s+ω^2 ))} I=(2/(ω(1−ω))){∫(dθ/(sin θ+ω))−∫(dθ/(sin θ+ω^2 ))} now its a piece of cake, just for cortano sir.
$${I}=\mathrm{2}\int\frac{\frac{{dx}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{1}+\sqrt{{x}}\sqrt{{x}+\mathrm{1}}} \\ $$$${let}\:\:\sqrt{{x}}={t}\:\:\Rightarrow\:\:\frac{{dx}}{\mathrm{2}\sqrt{{x}}}={dt} \\ $$$${I}=\mathrm{2}\int\frac{{dt}}{\mathrm{1}+{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${let}\:\:{t}=\mathrm{tan}\:\theta \\ $$$${I}=\mathrm{2}\int\frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{1}+\mathrm{sec}\:\theta\mathrm{tan}\:\theta} \\ $$$${I}=\mathrm{2}\int\frac{{d}\theta}{\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{sin}\:\theta} \\ $$$${I}=−\mathrm{2}\int\frac{{d}\theta}{\mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{sin}\:\theta+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{s}^{\mathrm{2}} −{s}+\mathrm{1}}=\frac{\mathrm{1}}{\omega\left(\omega−\mathrm{1}\right)}\left\{\frac{\mathrm{1}}{{s}+\omega}−\frac{\mathrm{1}}{{s}+\omega^{\mathrm{2}} }\right\} \\ $$$${I}=\frac{\mathrm{2}}{\omega\left(\mathrm{1}−\omega\right)}\left\{\int\frac{{d}\theta}{\mathrm{sin}\:\theta+\omega}−\int\frac{{d}\theta}{\mathrm{sin}\:\theta+\omega^{\mathrm{2}} }\right\} \\ $$$${now}\:{its}\:{a}\:{piece}\:{of}\:{cake}, \\ $$$${just}\:{for}\:{cortano}\:{sir}. \\ $$$$ \\ $$
Commented by cortano last updated on 22/Oct/21
waw that′s so sweet sir ajfour
$${waw}\:{that}'{s}\:{so}\:{sweet}\:{sir}\:{ajfour} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *