Question Number 125416 by bemath last updated on 10/Dec/20
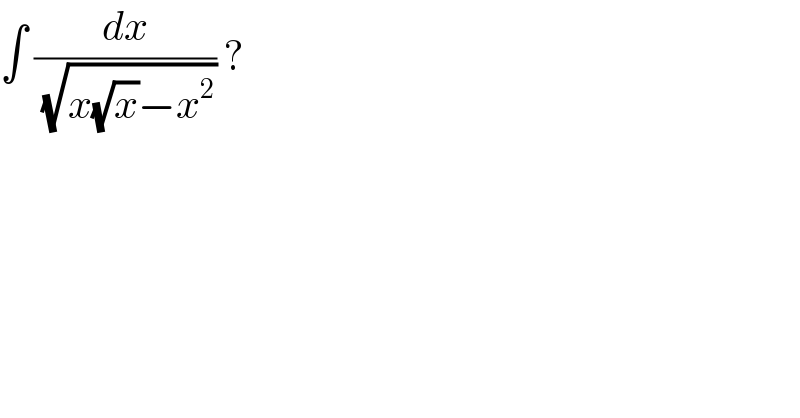
$$\int\:\frac{{dx}}{\:\sqrt{{x}\sqrt{{x}}−{x}^{\mathrm{2}} }}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 10/Dec/20
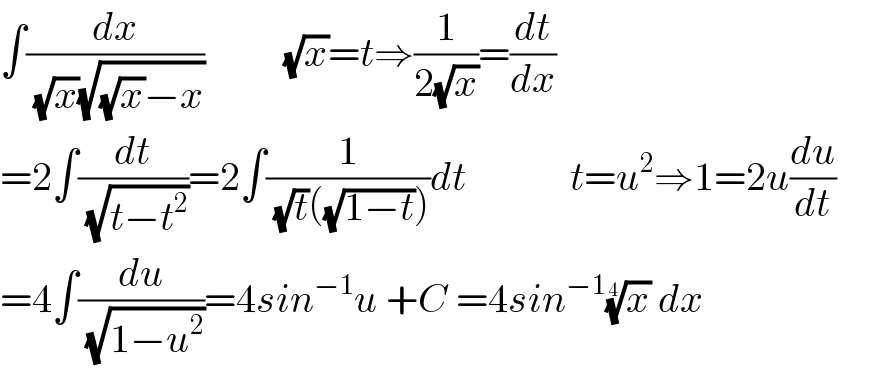
$$\int\frac{{dx}}{\:\sqrt{{x}}\sqrt{\sqrt{{x}}−{x}}}\:\:\:\:\:\:\:\:\:\:\sqrt{{x}}={t}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}=\frac{{dt}}{{dx}} \\ $$$$=\mathrm{2}\int\frac{{dt}}{\:\sqrt{{t}−{t}^{\mathrm{2}} }}=\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{{t}}\left(\sqrt{\mathrm{1}−{t}}\right)}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:{t}={u}^{\mathrm{2}} \Rightarrow\mathrm{1}=\mathrm{2}{u}\frac{{du}}{{dt}}\:\:\:\:\: \\ $$$$=\mathrm{4}\int\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}=\mathrm{4}{sin}^{−\mathrm{1}} {u}\:+{C}\:=\mathrm{4}{sin}^{−\mathrm{1}} \sqrt[{\mathrm{4}}]{{x}}\:{dx} \\ $$
Answered by liberty last updated on 10/Dec/20
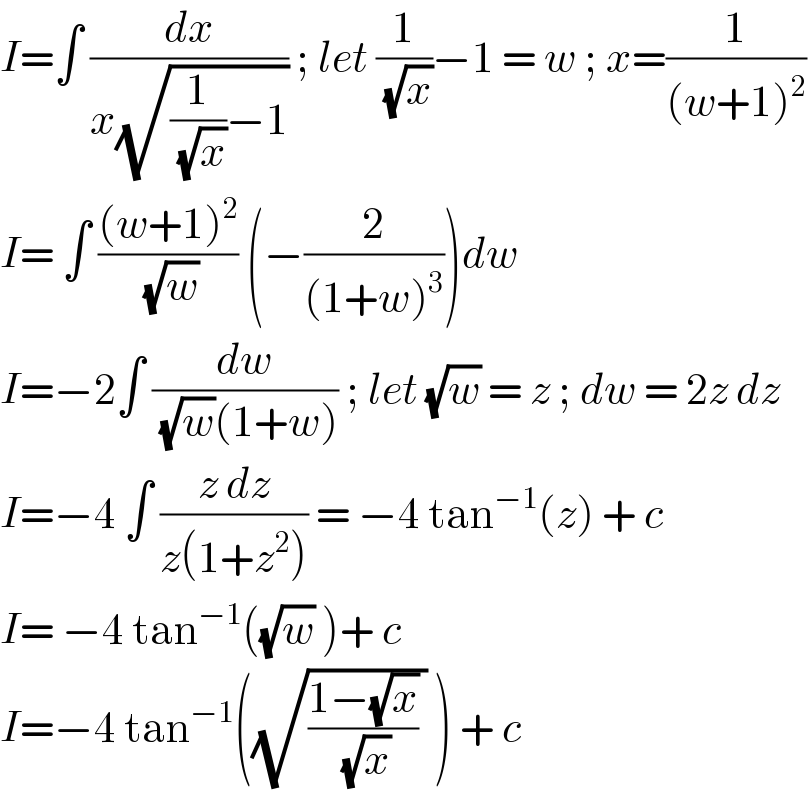
$${I}=\int\:\frac{{dx}}{{x}\sqrt{\frac{\mathrm{1}}{\:\sqrt{{x}}}−\mathrm{1}}}\:;\:{let}\:\frac{\mathrm{1}}{\:\sqrt{{x}}}−\mathrm{1}\:=\:{w}\:;\:{x}=\frac{\mathrm{1}}{\left({w}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}=\:\int\:\frac{\left({w}+\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{{w}}}\:\left(−\frac{\mathrm{2}}{\left(\mathrm{1}+{w}\right)^{\mathrm{3}} }\right){dw} \\ $$$${I}=−\mathrm{2}\int\:\frac{{dw}}{\:\sqrt{{w}}\left(\mathrm{1}+{w}\right)}\:;\:{let}\:\sqrt{{w}}\:=\:{z}\:;\:{dw}\:=\:\mathrm{2}{z}\:{dz} \\ $$$${I}=−\mathrm{4}\:\int\:\frac{{z}\:{dz}}{{z}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:=\:−\mathrm{4}\:\mathrm{tan}^{−\mathrm{1}} \left({z}\right)\:+\:{c} \\ $$$${I}=\:−\mathrm{4}\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{{w}}\:\right)+\:{c}\: \\ $$$${I}=−\mathrm{4}\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−\sqrt{{x}}}{\:\sqrt{{x}}}\:}\:\right)\:+\:{c}\: \\ $$
