Question Number 151341 by peter frank last updated on 20/Aug/21
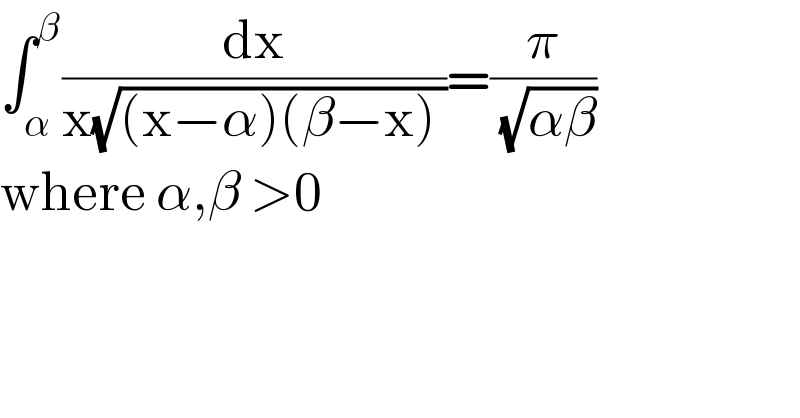
$$\int_{\alpha} ^{\beta} \frac{\mathrm{dx}}{\mathrm{x}\sqrt{\left(\mathrm{x}−\alpha\right)\left(\beta−\mathrm{x}\right)\:}}=\frac{\pi}{\:\sqrt{\alpha\beta}} \\ $$$$\mathrm{where}\:\alpha,\beta\:>\mathrm{0} \\ $$
Answered by Kamel last updated on 20/Aug/21
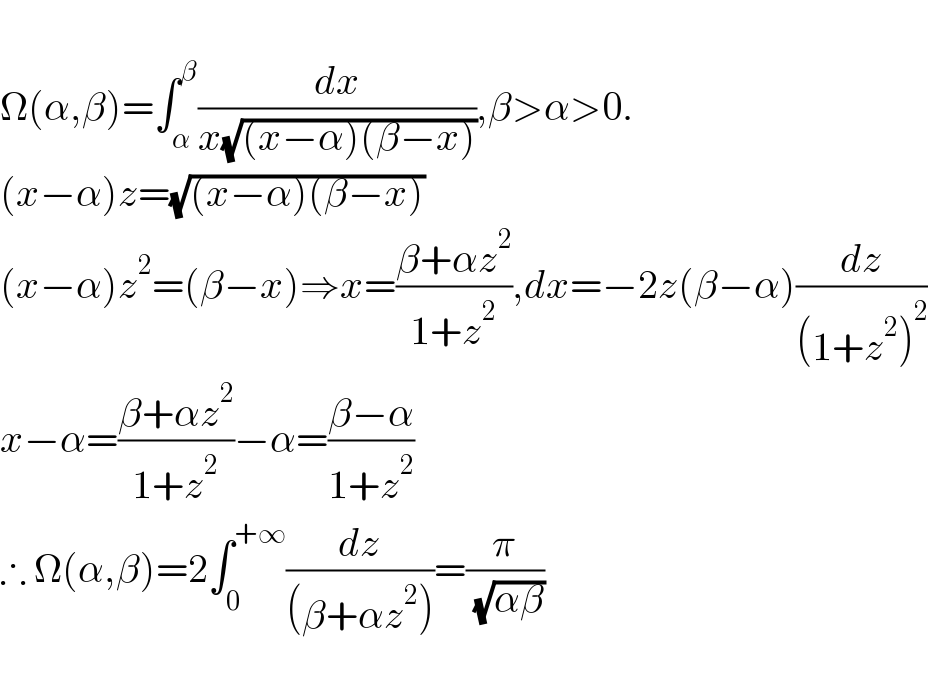
$$ \\ $$$$\Omega\left(\alpha,\beta\right)=\int_{\alpha} ^{\beta} \frac{{dx}}{{x}\sqrt{\left({x}−\alpha\right)\left(\beta−{x}\right)}},\beta>\alpha>\mathrm{0}. \\ $$$$\left({x}−\alpha\right){z}=\sqrt{\left({x}−\alpha\right)\left(\beta−{x}\right)} \\ $$$$\left({x}−\alpha\right){z}^{\mathrm{2}} =\left(\beta−{x}\right)\Rightarrow{x}=\frac{\beta+\alpha{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} },{dx}=−\mathrm{2}{z}\left(\beta−\alpha\right)\frac{{dz}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${x}−\alpha=\frac{\beta+\alpha{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }−\alpha=\frac{\beta−\alpha}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$\therefore\:\Omega\left(\alpha,\beta\right)=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{{dz}}{\left(\beta+\alpha{z}^{\mathrm{2}} \right)}=\frac{\pi}{\:\sqrt{\alpha\beta}} \\ $$$$ \\ $$
