Question Number 83713 by mhmd last updated on 05/Mar/20
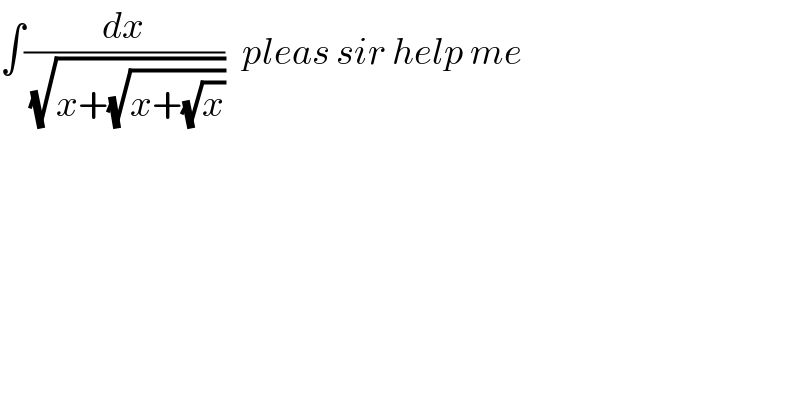
$$\int\frac{{dx}}{\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}}\:\:\:{pleas}\:{sir}\:{help}\:{me} \\ $$
Commented by niroj last updated on 05/Mar/20
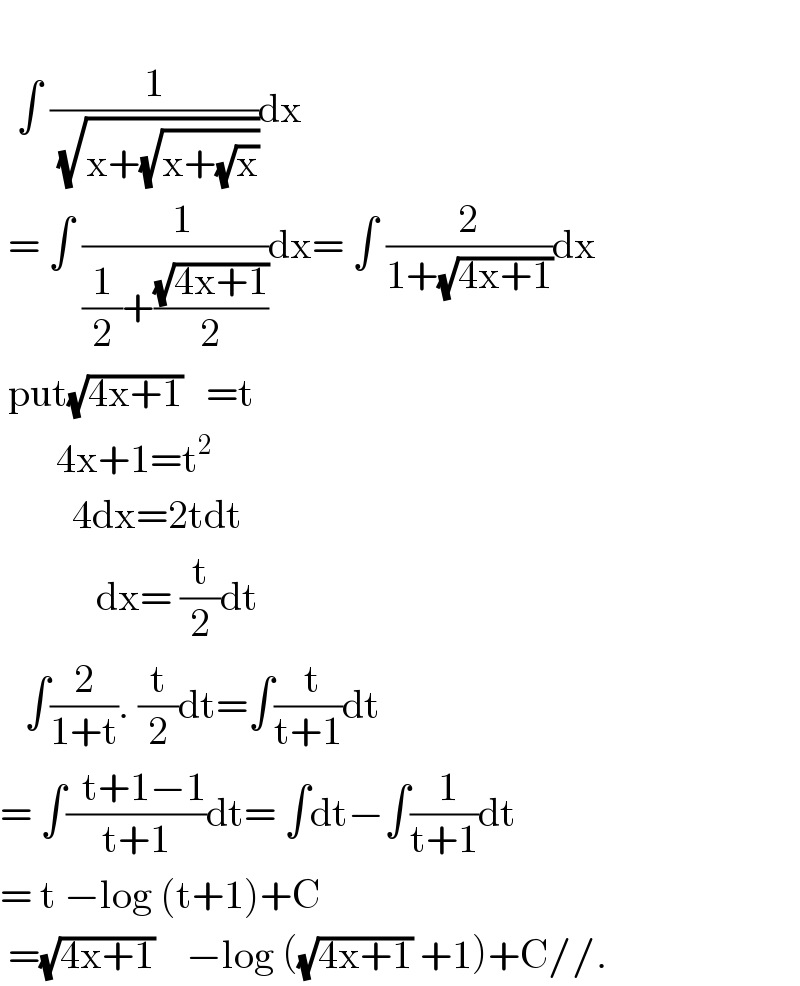
$$ \\ $$$$\:\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}\mathrm{dx} \\ $$$$\:=\:\int\:\frac{\:\:\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{4x}+\mathrm{1}}}{\mathrm{2}}}\mathrm{dx}=\:\int\:\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{4x}+\mathrm{1}}}\mathrm{dx} \\ $$$$\:\mathrm{put}\sqrt{\mathrm{4x}+\mathrm{1}}\:\:\:=\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\mathrm{4x}+\mathrm{1}=\mathrm{t}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{4dx}=\mathrm{2tdt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{dx}=\:\frac{\mathrm{t}}{\mathrm{2}}\mathrm{dt} \\ $$$$\:\:\:\int\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}}.\:\frac{\mathrm{t}}{\mathrm{2}}\mathrm{dt}=\int\frac{\:\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=\:\int\frac{\:\:\mathrm{t}+\mathrm{1}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mathrm{dt}=\:\int\mathrm{dt}−\int\frac{\:\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=\:\mathrm{t}\:−\mathrm{log}\:\left(\mathrm{t}+\mathrm{1}\right)+\mathrm{C} \\ $$$$\:=\sqrt{\mathrm{4x}+\mathrm{1}}\:\:\:\:−\mathrm{log}\:\left(\sqrt{\mathrm{4x}+\mathrm{1}}\:+\mathrm{1}\right)+\mathrm{C}//. \\ $$
Commented by MJS last updated on 05/Mar/20
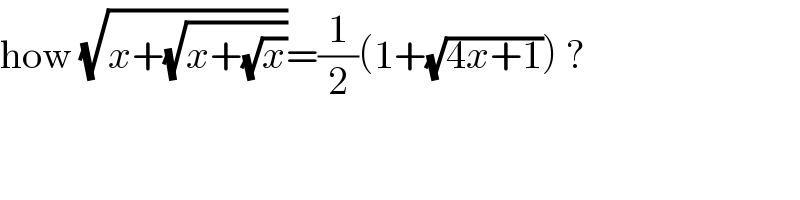
$$\mathrm{how}\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{4}{x}+\mathrm{1}}\right)\:? \\ $$
Commented by mhmd last updated on 05/Mar/20
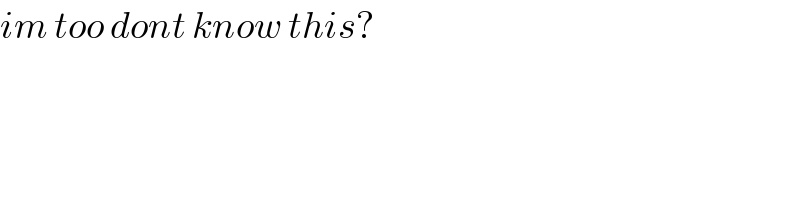
$${im}\:{too}\:{dont}\:{know}\:{this}? \\ $$
Commented by jagoll last updated on 05/Mar/20

$$??? \\ $$
Commented by mhmd last updated on 05/Mar/20
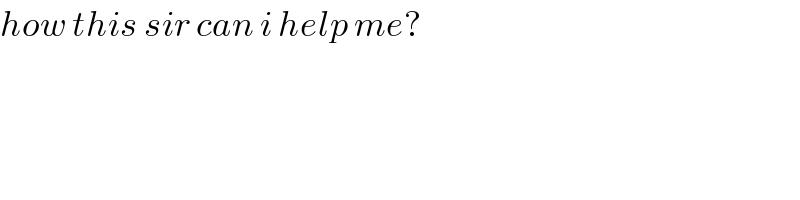
$${how}\:{this}\:{sir}\:{can}\:{i}\:{help}\:{me}? \\ $$
Commented by MJS last updated on 05/Mar/20

$$\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+…}}}\:\mathrm{to}\:\mathrm{infinity}: \\ $$$${y}=\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+…}}} \\ $$$${y}^{\mathrm{2}} ={x}+{y} \\ $$$$\Rightarrow\:{y}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}{x}+\mathrm{1}} \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}\:\mathrm{I}'\mathrm{m}\:\mathrm{afraid}\:\mathrm{we}\:\mathrm{cannot} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{integral} \\ $$
Commented by jagoll last updated on 05/Mar/20
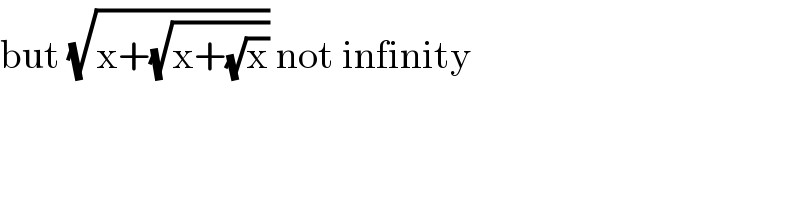
$$\mathrm{but}\:\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}\:\mathrm{not}\:\mathrm{infinity} \\ $$
Commented by MJS last updated on 05/Mar/20

$$\mathrm{yes}.\:\Rightarrow\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{it} \\ $$
Answered by msup trace by abdo last updated on 05/Mar/20
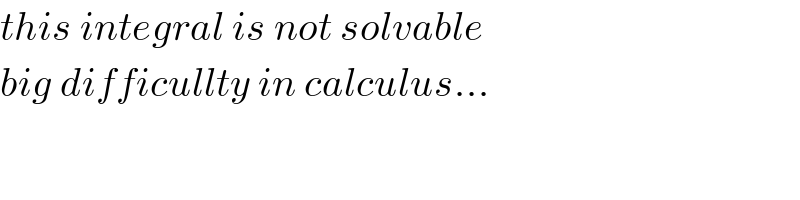
$${this}\:{integral}\:{is}\:{not}\:{solvable} \\ $$$${big}\:{difficullty}\:{in}\:{calculus}… \\ $$
