Question Number 161381 by mkam last updated on 17/Dec/21

$$\int\:\frac{{dy}}{\:\sqrt{{ae}^{{y}} +\mathrm{1}}} \\ $$
Answered by MohammadAzad last updated on 17/Dec/21
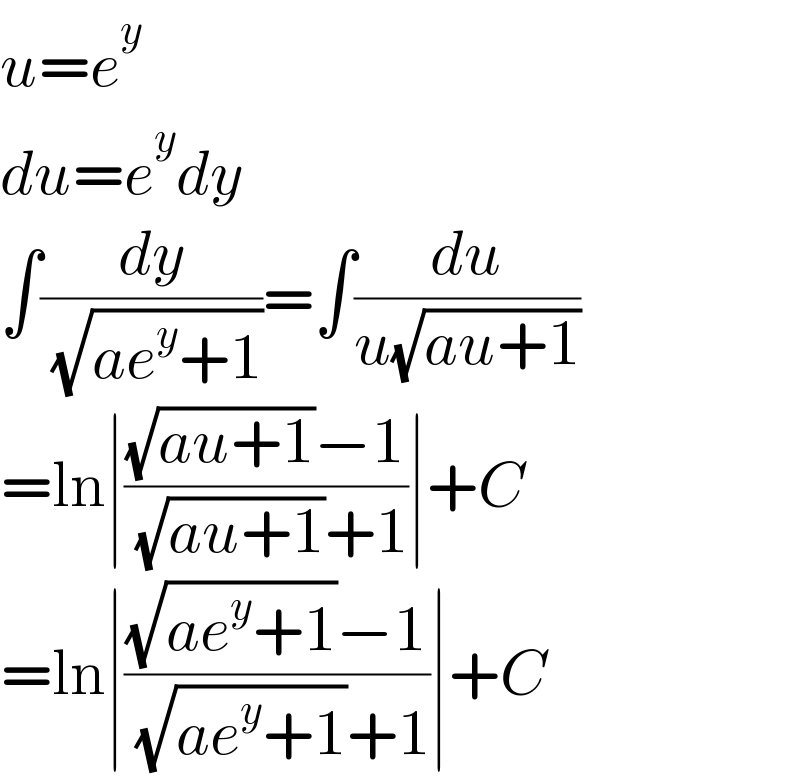
$${u}={e}^{{y}} \\ $$$${du}={e}^{{y}} {dy} \\ $$$$\int\frac{{dy}}{\:\sqrt{{ae}^{{y}} +\mathrm{1}}}=\int\frac{{du}}{{u}\sqrt{{au}+\mathrm{1}}} \\ $$$$=\mathrm{ln}\mid\frac{\sqrt{{au}+\mathrm{1}}−\mathrm{1}}{\:\sqrt{{au}+\mathrm{1}}+\mathrm{1}}\mid+{C} \\ $$$$=\mathrm{ln}\mid\frac{\sqrt{{ae}^{{y}} +\mathrm{1}}−\mathrm{1}}{\:\sqrt{{ae}^{{y}} +\mathrm{1}}+\mathrm{1}}\mid+{C} \\ $$
