Question Number 105238 by bemath last updated on 27/Jul/20
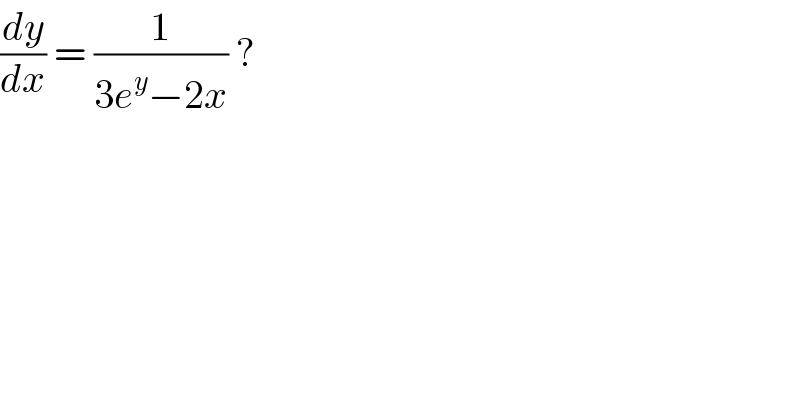
$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}{e}^{{y}} −\mathrm{2}{x}}\:? \\ $$
Answered by john santu last updated on 27/Jul/20
![(dx/dy) = 3e^y −2x (dx/dy) + 2x = 3e^y integrating factor u(y) = e^(∫2 dy) = e^(2y) ⇔e^(2y) (dx/dy) + 2xe^(2y) = 3e^(3y) (d/dy) [ x.e^(2y) ] = 3e^(3y) ∫ (d/dy)[x.e^(2y) ] dy = ∫ 3e^(3y) dy x.e^(2y) = e^(3y) + C ∴ x = e^y + Ce^(−3y) (JS ♠⧫)](https://www.tinkutara.com/question/Q105259.png)
$$\frac{{dx}}{{dy}}\:=\:\mathrm{3}{e}^{{y}} −\mathrm{2}{x}\: \\ $$$$\frac{{dx}}{{dy}}\:+\:\mathrm{2}{x}\:=\:\mathrm{3}{e}^{{y}} \\ $$$${integrating}\:{factor}\: \\ $$$${u}\left({y}\right)\:=\:{e}^{\int\mathrm{2}\:{dy}} \:=\:{e}^{\mathrm{2}{y}} \\ $$$$\Leftrightarrow{e}^{\mathrm{2}{y}} \:\frac{{dx}}{{dy}}\:+\:\mathrm{2}{xe}^{\mathrm{2}{y}} \:=\:\mathrm{3}{e}^{\mathrm{3}{y}} \\ $$$$\frac{{d}}{{dy}}\:\left[\:{x}.{e}^{\mathrm{2}{y}} \:\right]\:=\:\mathrm{3}{e}^{\mathrm{3}{y}} \\ $$$$\int\:\frac{{d}}{{dy}}\left[{x}.{e}^{\mathrm{2}{y}} \right]\:{dy}\:=\:\int\:\mathrm{3}{e}^{\mathrm{3}{y}} \:{dy} \\ $$$${x}.{e}^{\mathrm{2}{y}} \:=\:{e}^{\mathrm{3}{y}} \:+\:{C}\: \\ $$$$\therefore\:{x}\:=\:{e}^{{y}} \:+\:{Ce}^{−\mathrm{3}{y}} \: \\ $$$$\left({JS}\:\spadesuit\blacklozenge\right) \\ $$
