Question Number 104240 by bemath last updated on 20/Jul/20
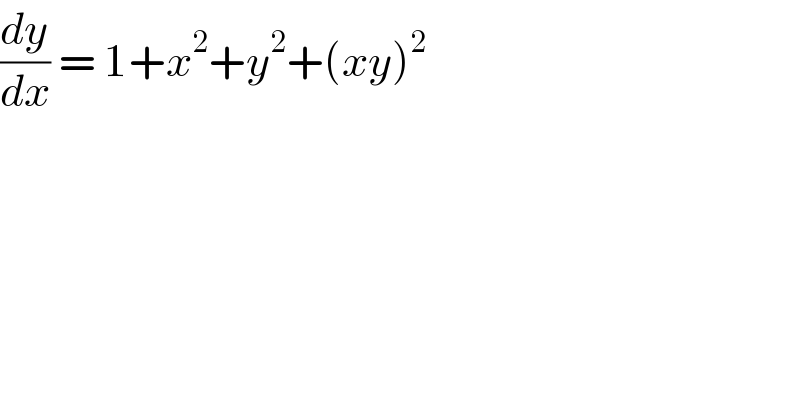
$$\frac{{dy}}{{dx}}\:=\:\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({xy}\right)^{\mathrm{2}} \\ $$
Commented by bemath last updated on 20/Jul/20
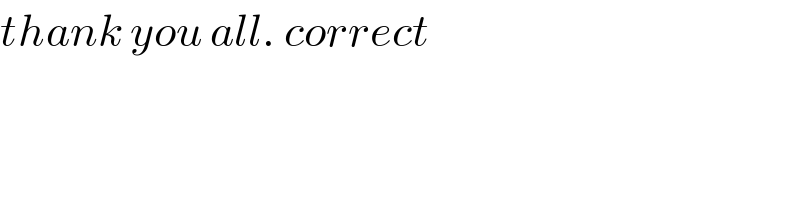
$${thank}\:{you}\:{all}.\:{correct} \\ $$
Answered by OlafThorendsen last updated on 20/Jul/20
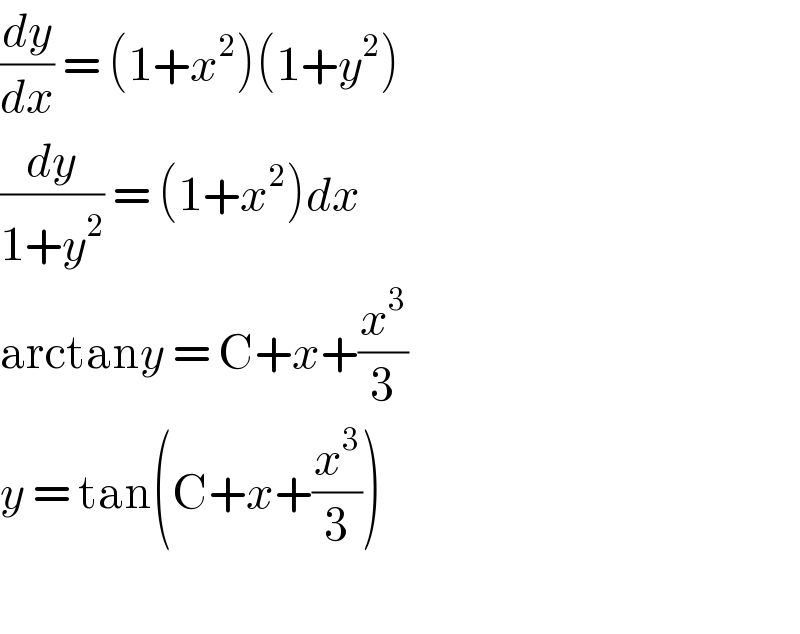
$$\frac{{dy}}{{dx}}\:=\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{y}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }\:=\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{arctan}{y}\:=\:\mathrm{C}+{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$${y}\:=\:\mathrm{tan}\left(\mathrm{C}+{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 20/Jul/20

$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} =\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\frac{\mathrm{dy}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}.\mathrm{Integrate}\:\mathrm{two} \\ $$$$\mathrm{sides}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{arctan}\:\mathrm{y}=\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{C}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{tan}\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)+\mathrm{C} \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{correct},\mathrm{Sir}?.\mathrm{Please}\:\mathrm{check}\:\mathrm{to}\:\mathrm{help} \\ $$$$\mathrm{me}. \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jul/20

$$\frac{\mathrm{dy}}{\mathrm{dx}}=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right) \\ $$$$\int\frac{\mathrm{dy}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }=\int\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \mathrm{y}=\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{C}_{\mathrm{1}} \right) \\ $$$$\mathrm{y}=\mathrm{tan}\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{C}_{\mathrm{1}} \right) \\ $$
