Menu Close

dy-dx-2x-2-y-2-3x-2-2xy-

Tinku Tara 0 Comments
Pin




Question Number 90810 by john santu last updated on 26/Apr/20
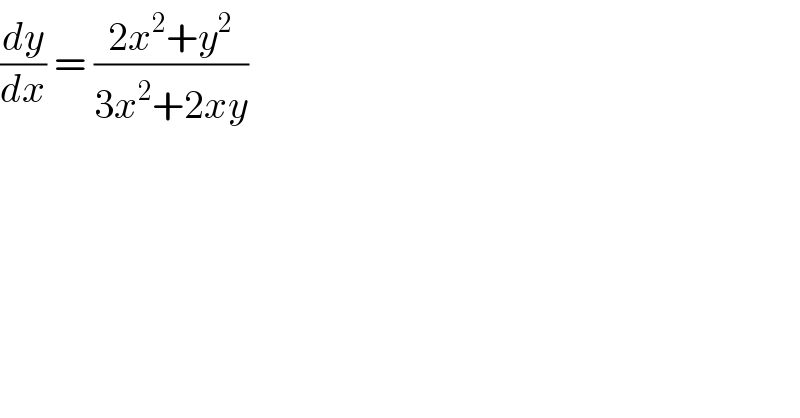
(dy/dx) = ((2x^2 +y^2 )/(3x^2 +2xy))
$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{xy}}\: \\ $$
Commented by peter frank last updated on 26/Apr/20
help Qn 90812
$${help}\:{Qn}\:\:\mathrm{90812} \\ $$
Commented by john santu last updated on 26/Apr/20
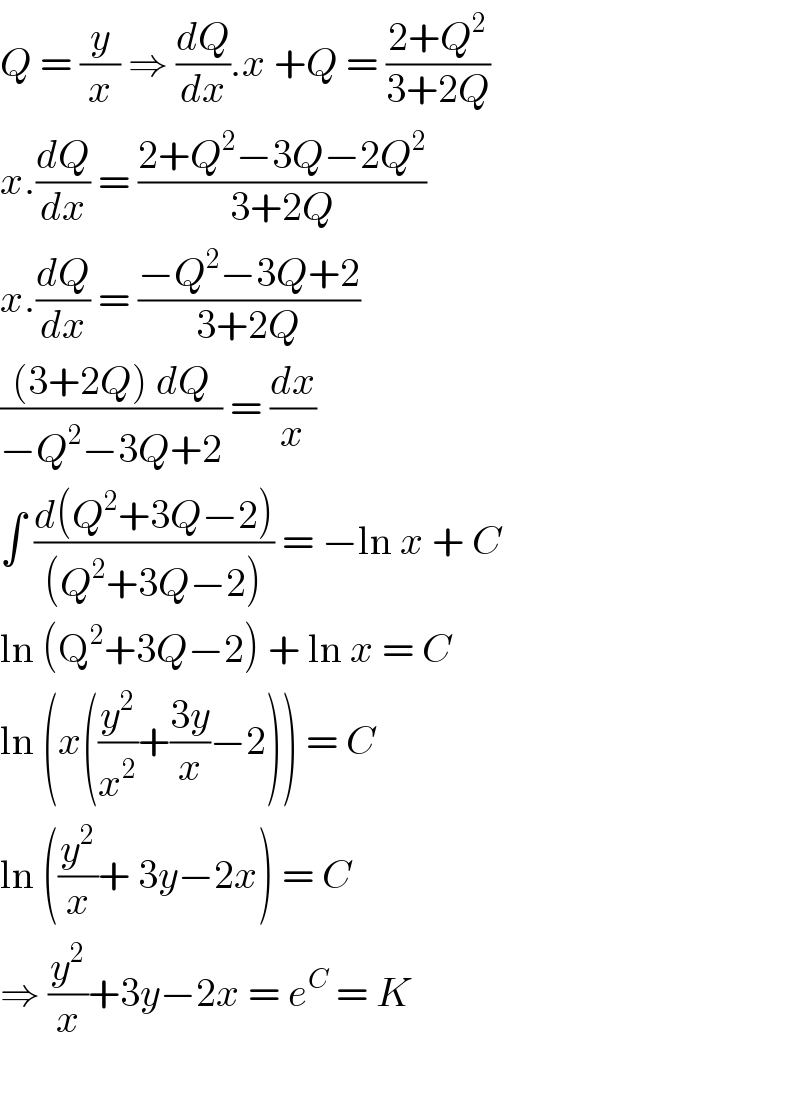
Q = (y/x) ⇒ (dQ/dx).x +Q = ((2+Q^2 )/(3+2Q)) x.(dQ/dx) = ((2+Q^2 −3Q−2Q^2 )/(3+2Q)) x.(dQ/dx) = ((−Q^2 −3Q+2)/(3+2Q)) (((3+2Q) dQ)/(−Q^2 −3Q+2)) = (dx/x) ∫ ((d(Q^2 +3Q−2))/((Q^2 +3Q−2))) = −ln x + C ln (Q^2 +3Q−2) + ln x = C ln (x((y^2 /x^2 )+((3y)/x)−2)) = C ln ((y^2 /x)+ 3y−2x) = C ⇒ (y^2 /x)+3y−2x = e^C = K
$${Q}\:=\:\frac{{y}}{{x}}\:\Rightarrow\:\frac{{dQ}}{{dx}}.{x}\:+{Q}\:=\:\frac{\mathrm{2}+{Q}^{\mathrm{2}} }{\mathrm{3}+\mathrm{2}{Q}} \\ $$$${x}.\frac{{dQ}}{{dx}}\:=\:\frac{\mathrm{2}+{Q}^{\mathrm{2}} −\mathrm{3}{Q}−\mathrm{2}{Q}^{\mathrm{2}} }{\mathrm{3}+\mathrm{2}{Q}} \\ $$$${x}.\frac{{dQ}}{{dx}}\:=\:\frac{−{Q}^{\mathrm{2}} −\mathrm{3}{Q}+\mathrm{2}}{\mathrm{3}+\mathrm{2}{Q}} \\ $$$$\frac{\left(\mathrm{3}+\mathrm{2}{Q}\right)\:{dQ}}{−{Q}^{\mathrm{2}} −\mathrm{3}{Q}+\mathrm{2}}\:=\:\frac{{dx}}{{x}} \\ $$$$\int\:\frac{{d}\left({Q}^{\mathrm{2}} +\mathrm{3}{Q}−\mathrm{2}\right)}{\left({Q}^{\mathrm{2}} +\mathrm{3}{Q}−\mathrm{2}\right)}\:=\:−\mathrm{ln}\:{x}\:+\:{C} \\ $$$$\mathrm{ln}\:\left(\mathrm{Q}^{\mathrm{2}} +\mathrm{3}{Q}−\mathrm{2}\right)\:+\:\mathrm{ln}\:{x}\:=\:{C} \\ $$$$\mathrm{ln}\:\left({x}\left(\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{\mathrm{3}{y}}{{x}}−\mathrm{2}\right)\right)\:=\:{C} \\ $$$$\mathrm{ln}\:\left(\frac{{y}^{\mathrm{2}} }{{x}}+\:\mathrm{3}{y}−\mathrm{2}{x}\right)\:=\:{C} \\ $$$$\Rightarrow\:\frac{{y}^{\mathrm{2}} }{{x}}+\mathrm{3}{y}−\mathrm{2}{x}\:=\:{e}^{{C}} \:=\:{K}\: \\ $$$$ \\ $$
Answered by Joel578 last updated on 26/Apr/20
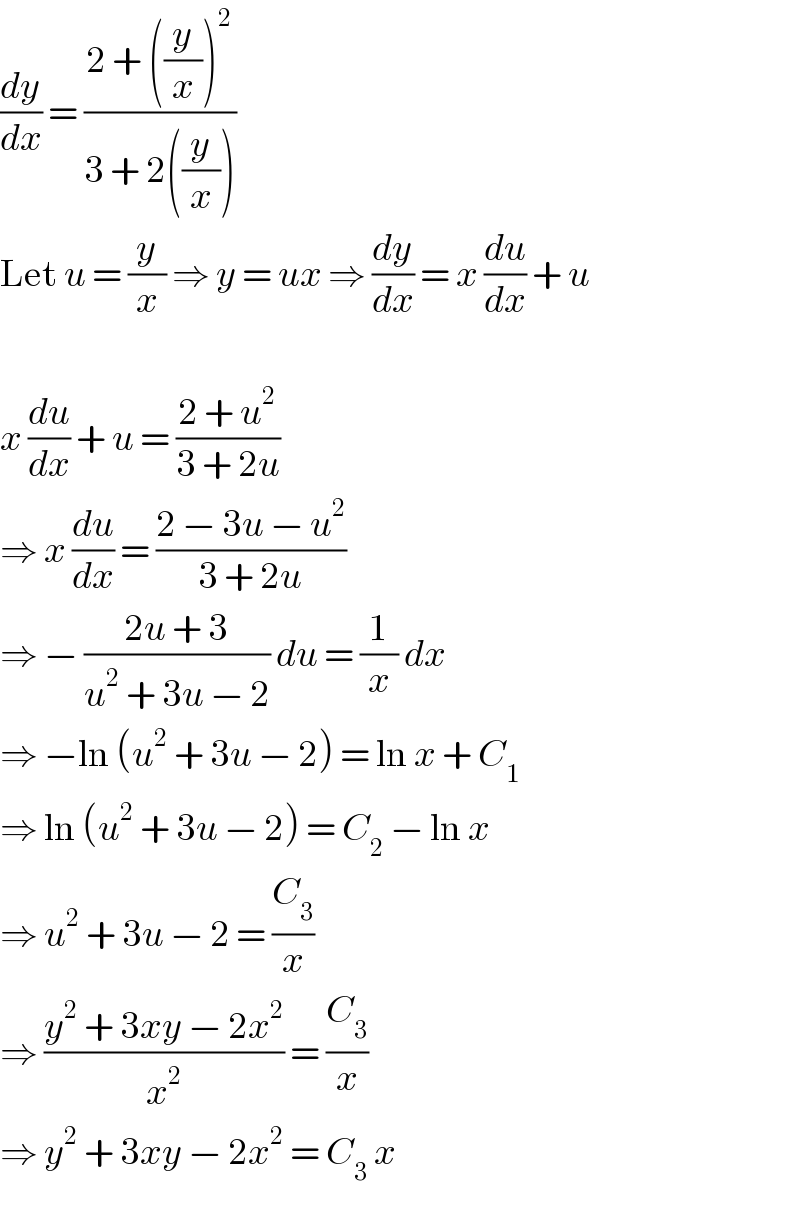
(dy/dx) = ((2 + ((y/x))^2 )/(3 + 2((y/x)))) Let u = (y/x) ⇒ y = ux ⇒ (dy/dx) = x (du/dx) + u x (du/dx) + u = ((2 + u^2 )/(3 + 2u)) ⇒ x (du/dx) = ((2 − 3u − u^2 )/(3 + 2u)) ⇒ − ((2u + 3)/(u^2 + 3u − 2)) du = (1/x) dx ⇒ −ln (u^2 + 3u − 2) = ln x + C_1 ⇒ ln (u^2 + 3u − 2) = C_2 − ln x ⇒ u^2 + 3u − 2 = (C_3 /x) ⇒ ((y^2 + 3xy − 2x^2 )/x^2 ) = (C_3 /x) ⇒ y^2 + 3xy − 2x^2 = C_3 x
$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}\:+\:\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }{\mathrm{3}\:+\:\mathrm{2}\left(\frac{{y}}{{x}}\right)} \\ $$$$\mathrm{Let}\:{u}\:=\:\frac{{y}}{{x}}\:\Rightarrow\:{y}\:=\:{ux}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{x}\:\frac{{du}}{{dx}}\:+\:{u} \\ $$$$ \\ $$$${x}\:\frac{{du}}{{dx}}\:+\:{u}\:=\:\frac{\mathrm{2}\:+\:{u}^{\mathrm{2}} }{\mathrm{3}\:+\:\mathrm{2}{u}} \\ $$$$\Rightarrow\:{x}\:\frac{{du}}{{dx}}\:=\:\frac{\mathrm{2}\:−\:\mathrm{3}{u}\:−\:{u}^{\mathrm{2}} }{\mathrm{3}\:+\:\mathrm{2}{u}} \\ $$$$\Rightarrow\:−\:\frac{\mathrm{2}{u}\:+\:\mathrm{3}}{{u}^{\mathrm{2}} \:+\:\mathrm{3}{u}\:−\:\mathrm{2}}\:{du}\:=\:\frac{\mathrm{1}}{{x}}\:{dx} \\ $$$$\Rightarrow\:−\mathrm{ln}\:\left({u}^{\mathrm{2}} \:+\:\mathrm{3}{u}\:−\:\mathrm{2}\right)\:=\:\mathrm{ln}\:{x}\:+\:{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{ln}\:\left({u}^{\mathrm{2}} \:+\:\mathrm{3}{u}\:−\:\mathrm{2}\right)\:=\:{C}_{\mathrm{2}} \:−\:\mathrm{ln}\:{x} \\ $$$$\Rightarrow\:{u}^{\mathrm{2}} \:+\:\mathrm{3}{u}\:−\:\mathrm{2}\:=\:\frac{{C}_{\mathrm{3}} }{{x}} \\ $$$$\Rightarrow\:\frac{{y}^{\mathrm{2}} \:+\:\mathrm{3}{xy}\:−\:\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\:\frac{{C}_{\mathrm{3}} }{{x}} \\ $$$$\Rightarrow\:{y}^{\mathrm{2}} \:+\:\mathrm{3}{xy}\:−\:\mathrm{2}{x}^{\mathrm{2}} \:=\:{C}_{\mathrm{3}} \:{x} \\ $$
Commented by peter frank last updated on 26/Apr/20
thanks
$${thanks} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *