Question Number 115539 by bemath last updated on 26/Sep/20
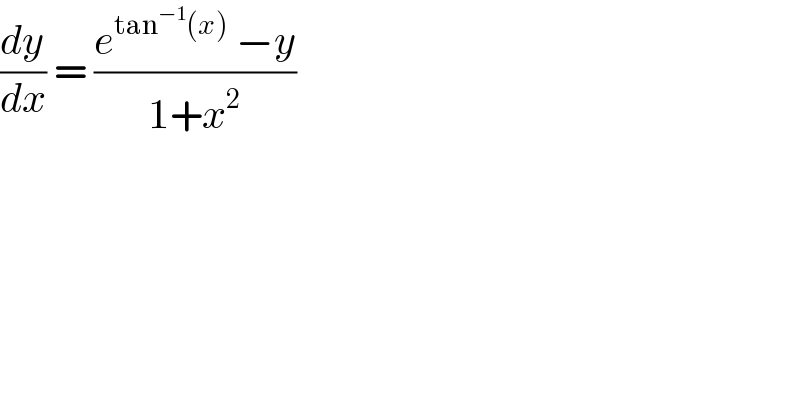
$$\frac{{dy}}{{dx}}\:=\:\frac{{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:−{y}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$
Answered by bobhans last updated on 26/Sep/20

$$\frac{{dy}}{{dx}}\:+\:\frac{{y}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\frac{{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${Integrating}\:{factor}\: \\ $$$${IF}\:=\:{e}^{\int\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }} \:=\:{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \\ $$$${solution}\::\:{y}.{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:=\:\int\:{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:.\frac{{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$${y}.{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:=\:\int\:\frac{{e}^{\mathrm{2tan}^{−\mathrm{1}} \left({x}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\: \\ $$$${set}\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)=\:{u}\:\Rightarrow{x}\:=\:\mathrm{tan}\:{u} \\ $$$$\int\:\frac{{e}^{\mathrm{2}{u}} }{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {u}}\:\mathrm{sec}\:^{\mathrm{2}} {u}\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{u}} +{c} \\ $$$$\therefore\:{y}.{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2tan}^{−\mathrm{1}} \left({x}\right)} \:+\:{c}\: \\ $$$${y}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:+\:{C}.{e}^{−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)} \:. \\ $$
