Question Number 92464 by jagoll last updated on 07/May/20
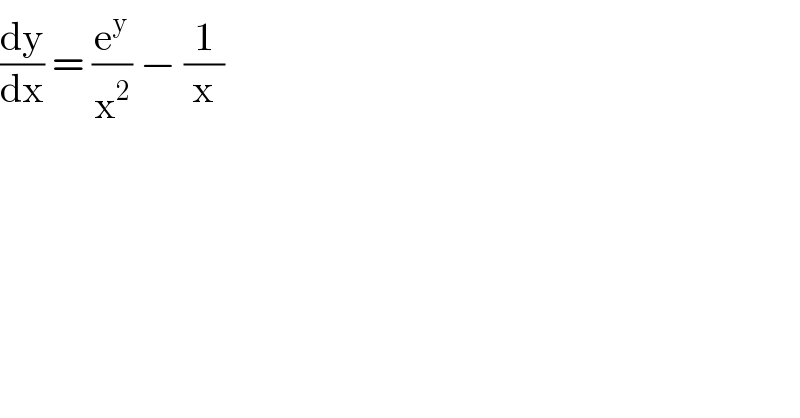
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{e}^{\mathrm{y}} }{\mathrm{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$
Commented by mr W last updated on 07/May/20
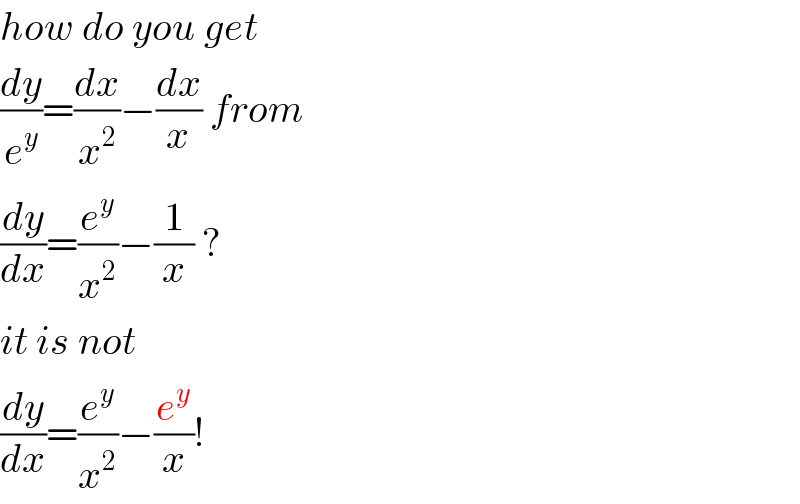
$${how}\:{do}\:{you}\:{get} \\ $$$$\frac{{dy}}{{e}^{{y}} }=\frac{{dx}}{{x}^{\mathrm{2}} }−\frac{{dx}}{{x}}\:{from} \\ $$$$\frac{{dy}}{{dx}}=\frac{{e}^{{y}} }{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}\:? \\ $$$${it}\:{is}\:{not} \\ $$$$\frac{{dy}}{{dx}}=\frac{{e}^{{y}} }{{x}^{\mathrm{2}} }−\frac{{e}^{{y}} }{{x}}! \\ $$
Commented by mathmax by abdo last updated on 07/May/20
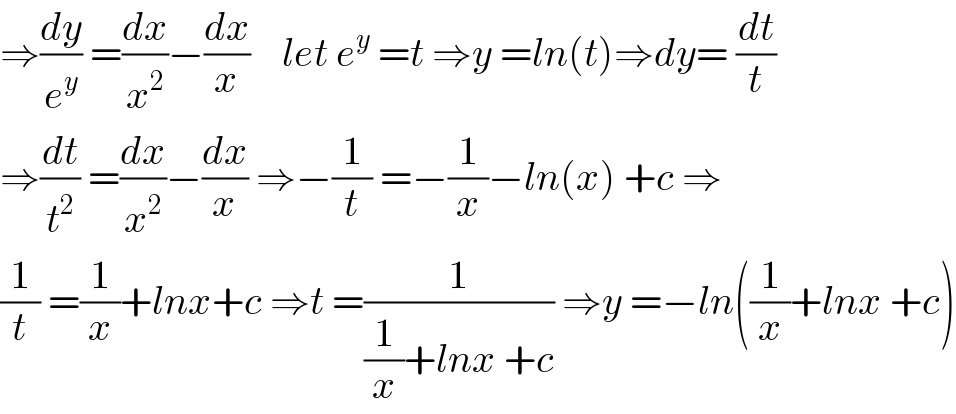
$$\Rightarrow\frac{{dy}}{{e}^{{y}} }\:=\frac{{dx}}{{x}^{\mathrm{2}} }−\frac{{dx}}{{x}}\:\:\:\:{let}\:{e}^{{y}} \:={t}\:\Rightarrow{y}\:={ln}\left({t}\right)\Rightarrow{dy}=\:\frac{{dt}}{{t}} \\ $$$$\Rightarrow\frac{{dt}}{{t}^{\mathrm{2}} }\:=\frac{{dx}}{{x}^{\mathrm{2}} }−\frac{{dx}}{{x}}\:\Rightarrow−\frac{\mathrm{1}}{{t}}\:=−\frac{\mathrm{1}}{{x}}−{ln}\left({x}\right)\:+{c}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{t}}\:=\frac{\mathrm{1}}{{x}}+{lnx}+{c}\:\Rightarrow{t}\:=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{x}}+{lnx}\:+{c}}\:\Rightarrow{y}\:=−{ln}\left(\frac{\mathrm{1}}{{x}}+{lnx}\:+{c}\right) \\ $$
Commented by i jagooll last updated on 16/May/20

$$\mathrm{mr}\:\mathrm{Abdo}.\:\mathrm{no}\:\mathrm{sir}.\:\mathrm{it}\:\mathrm{no}\:\mathrm{correct} \\ $$$$ \\ $$
Commented by i jagooll last updated on 16/May/20
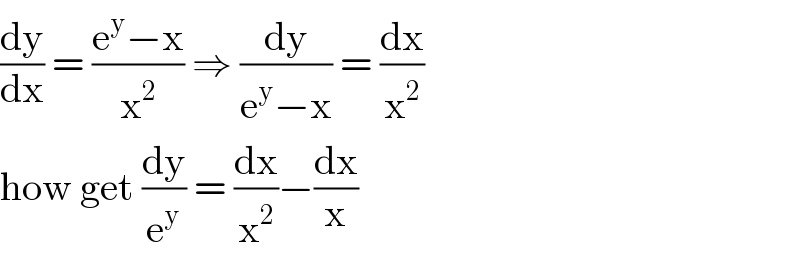
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{e}^{\mathrm{y}} −\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{e}^{\mathrm{y}} −\mathrm{x}}\:=\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{how}\:\mathrm{get}\:\frac{\mathrm{dy}}{\mathrm{e}^{\mathrm{y}} }\:=\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{dx}}{\mathrm{x}}\: \\ $$
