Question Number 85503 by john santu last updated on 22/Mar/20
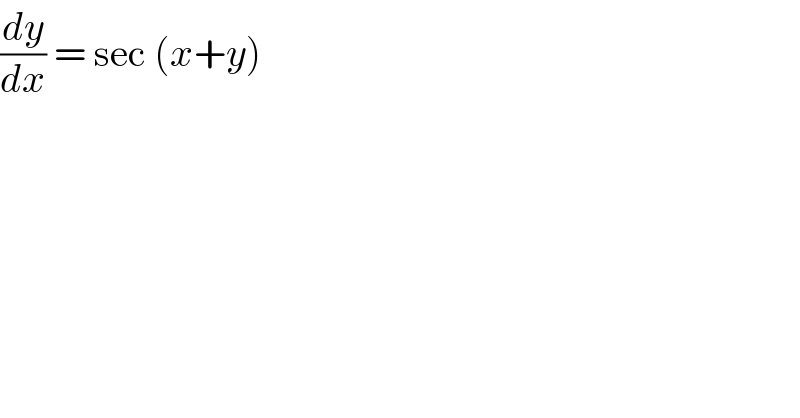
$$\frac{{dy}}{{dx}}\:=\:\mathrm{sec}\:\left({x}+{y}\right)\: \\ $$
Answered by mr W last updated on 22/Mar/20
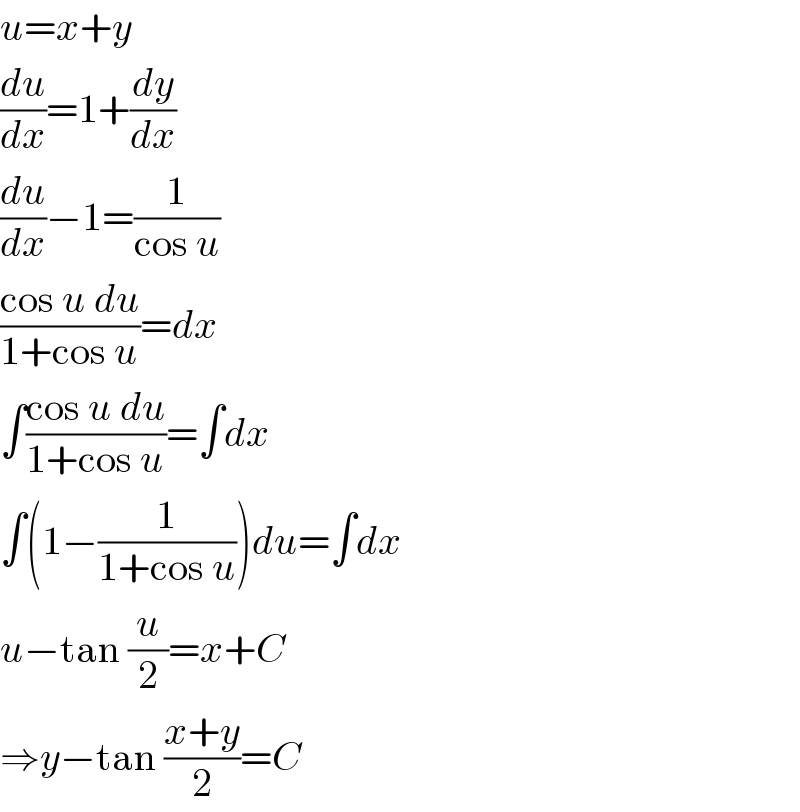
$${u}={x}+{y} \\ $$$$\frac{{du}}{{dx}}=\mathrm{1}+\frac{{dy}}{{dx}} \\ $$$$\frac{{du}}{{dx}}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{cos}\:{u}} \\ $$$$\frac{\mathrm{cos}\:{u}\:{du}}{\mathrm{1}+\mathrm{cos}\:{u}}={dx} \\ $$$$\int\frac{\mathrm{cos}\:{u}\:{du}}{\mathrm{1}+\mathrm{cos}\:{u}}=\int{dx} \\ $$$$\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:{u}}\right){du}=\int{dx} \\ $$$${u}−\mathrm{tan}\:\frac{{u}}{\mathrm{2}}={x}+{C} \\ $$$$\Rightarrow{y}−\mathrm{tan}\:\frac{{x}+{y}}{\mathrm{2}}={C} \\ $$
