Question Number 123280 by zarminaawan last updated on 24/Nov/20
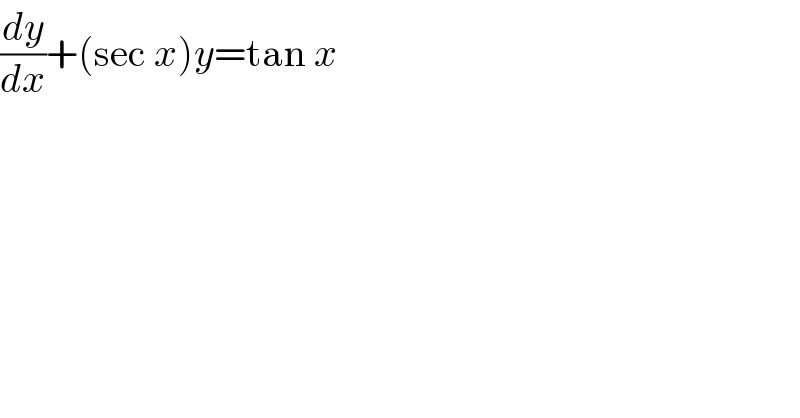
$$\frac{{dy}}{{dx}}+\left(\mathrm{sec}\:{x}\right){y}=\mathrm{tan}\:{x} \\ $$
Answered by Dwaipayan Shikari last updated on 24/Nov/20

$${I}.{F}={e}^{\int{secx}} ={secx}+{tanx} \\ $$$${y}\left({secx}+{tanx}\right)=\int{tanx}\left({secx}+{tanx}\right){dx} \\ $$$${y}\left({secx}+{tanx}\right)=\int{tanxsecx}+\int{tan}^{\mathrm{2}} {xdx} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\left({secx}+{tanx}\right)}\left({secx}+{tanx}−{x}+{C}\right)=\mathrm{1}+\frac{{C}−{x}}{{secx}+{tanx}} \\ $$
