Question Number 180976 by Mastermind last updated on 19/Nov/22

$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{x}−\mathrm{y}−\mathrm{2}}{\mathrm{x}+\mathrm{y}+\mathrm{6}} \\ $$$$ \\ $$$$\mathrm{solve} \\ $$
Answered by mr W last updated on 19/Nov/22
![x=u+a y=v+b x−y−2=u−v+a−b−2 x+y+6=u+v+a+b+6 a−b−2=0 a+b+6=0 ⇒a=−2, b=−4 ⇒x=u−2, y=v−4 (dy/dx)=(dv/du) (dv/du)=((u−v)/(u+v)) v=tu (dv/du)=t+u(dt/du)=((1−t)/(1+t)) u(dt/du)=((1−2t−t^2 )/(1+t)) (((t+1)dt)/(t^2 +2t−1))=−(du/u) (((t+1)dt)/((t+1)^2 −2))=−(du/u) ∫((d[(t+1)^2 −2])/((t+1)^2 −2))=−2∫(du/u) ln [(t+1)^2 −2]=−2ln u+C ⇒[(t+1)^2 −2]u^2 =C ⇒[((v/u)+1)^2 −2]u^2 =C ⇒[(((y+4)/(x+2))+1)^2 −2](x+2)^2 =C ⇒(x+y+6)^2 −2(x+2)^2 =C](https://www.tinkutara.com/question/Q180980.png)
$${x}={u}+{a} \\ $$$${y}={v}+{b} \\ $$$${x}−{y}−\mathrm{2}={u}−{v}+{a}−{b}−\mathrm{2} \\ $$$${x}+{y}+\mathrm{6}={u}+{v}+{a}+{b}+\mathrm{6} \\ $$$${a}−{b}−\mathrm{2}=\mathrm{0} \\ $$$${a}+{b}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow{a}=−\mathrm{2},\:{b}=−\mathrm{4} \\ $$$$\Rightarrow{x}={u}−\mathrm{2},\:{y}={v}−\mathrm{4} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dv}}{{du}} \\ $$$$\frac{{dv}}{{du}}=\frac{{u}−{v}}{{u}+{v}} \\ $$$${v}={tu} \\ $$$$\frac{{dv}}{{du}}={t}+{u}\frac{{dt}}{{du}}=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}} \\ $$$${u}\frac{{dt}}{{du}}=\frac{\mathrm{1}−\mathrm{2}{t}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}} \\ $$$$\frac{\left({t}+\mathrm{1}\right){dt}}{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}=−\frac{{du}}{{u}} \\ $$$$\frac{\left({t}+\mathrm{1}\right){dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}}=−\frac{{du}}{{u}} \\ $$$$\int\frac{{d}\left[\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right]}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}}=−\mathrm{2}\int\frac{{du}}{{u}} \\ $$$$\mathrm{ln}\:\left[\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right]=−\mathrm{2ln}\:{u}+{C} \\ $$$$\Rightarrow\left[\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right]{u}^{\mathrm{2}} ={C} \\ $$$$\Rightarrow\left[\left(\frac{{v}}{{u}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right]{u}^{\mathrm{2}} ={C} \\ $$$$\Rightarrow\left[\left(\frac{{y}+\mathrm{4}}{{x}+\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right]\left({x}+\mathrm{2}\right)^{\mathrm{2}} ={C} \\ $$$$\Rightarrow\left({x}+{y}+\mathrm{6}\right)^{\mathrm{2}} −\mathrm{2}\left({x}+\mathrm{2}\right)^{\mathrm{2}} ={C} \\ $$
Commented by Mastermind last updated on 19/Nov/22
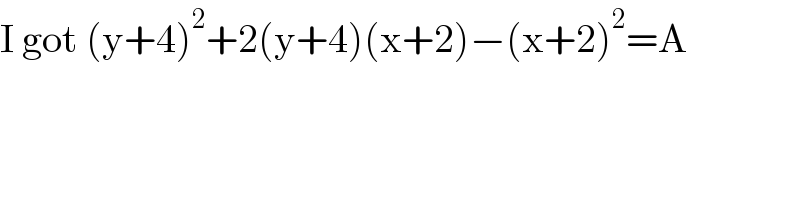
$$\mathrm{I}\:\mathrm{got}\:\left(\mathrm{y}+\mathrm{4}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{y}+\mathrm{4}\right)\left(\mathrm{x}+\mathrm{2}\right)−\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{A} \\ $$
Answered by qaz last updated on 20/Nov/22
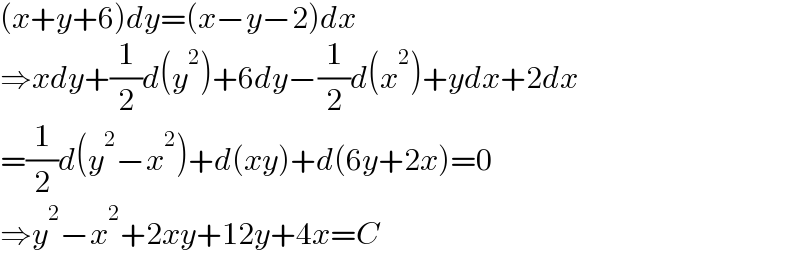
$$\left({x}+{y}+\mathrm{6}\right){dy}=\left({x}−{y}−\mathrm{2}\right){dx} \\ $$$$\Rightarrow{xdy}+\frac{\mathrm{1}}{\mathrm{2}}{d}\left({y}^{\mathrm{2}} \right)+\mathrm{6}{dy}−\frac{\mathrm{1}}{\mathrm{2}}{d}\left({x}^{\mathrm{2}} \right)+{ydx}+\mathrm{2}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{d}\left({y}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)+{d}\left({xy}\right)+{d}\left(\mathrm{6}{y}+\mathrm{2}{x}\right)=\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{12}{y}+\mathrm{4}{x}={C} \\ $$
