Menu Close

dy-dx-xy-2-2y-3-x-3-x-2-y-xy-2-Solve-

Tinku Tara 0 Comments
Pin




Question Number 181723 by Mastermind last updated on 29/Nov/22
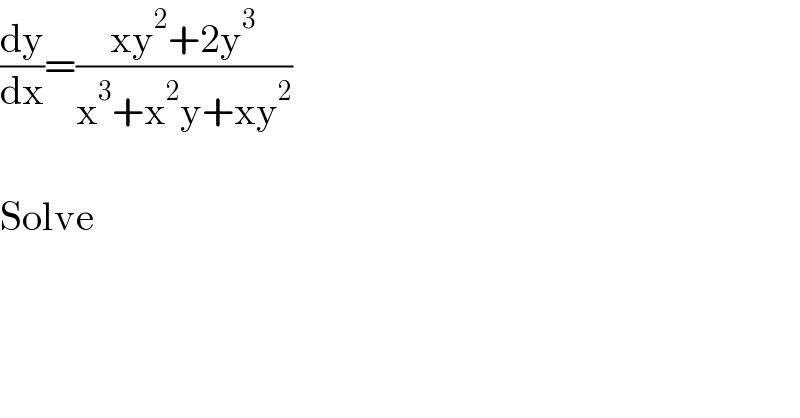
(dy/dx)=((xy^2 +2y^3 )/(x^3 +x^2 y+xy^2 )) Solve
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{xy}^{\mathrm{2}} +\mathrm{2y}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{xy}^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{Solve} \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 29/Nov/22
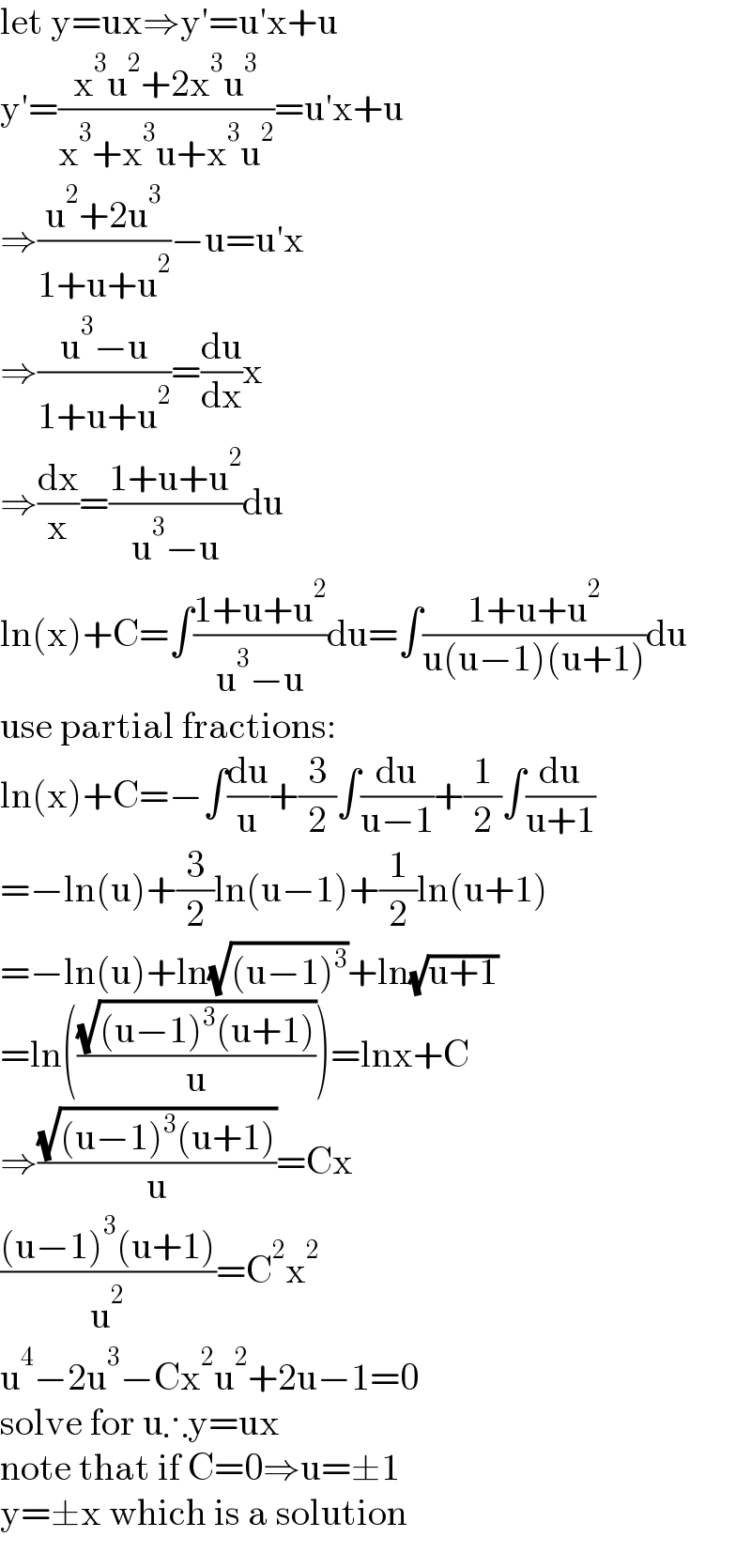
let y=ux⇒y′=u′x+u y′=((x^3 u^2 +2x^3 u^3 )/(x^3 +x^3 u+x^3 u^2 ))=u′x+u ⇒((u^2 +2u^3 )/(1+u+u^2 ))−u=u′x ⇒((u^3 −u)/(1+u+u^2 ))=(du/dx)x ⇒(dx/x)=((1+u+u^2 )/(u^3 −u))du ln(x)+C=∫((1+u+u^2 )/(u^3 −u))du=∫((1+u+u^2 )/(u(u−1)(u+1)))du use partial fractions: ln(x)+C=−∫(du/u)+(3/2)∫(du/(u−1))+(1/2)∫(du/(u+1)) =−ln(u)+(3/2)ln(u−1)+(1/2)ln(u+1) =−ln(u)+ln(√((u−1)^3 ))+ln(√(u+1)) =ln(((√((u−1)^3 (u+1)))/u))=lnx+C ⇒((√((u−1)^3 (u+1)))/u)=Cx (((u−1)^3 (u+1))/u^2 )=C^2 x^2 u^4 −2u^3 −Cx^2 u^2 +2u−1=0 solve for u∴y=ux note that if C=0⇒u=±1 y=±x which is a solution
$$\mathrm{let}\:\mathrm{y}=\mathrm{ux}\Rightarrow\mathrm{y}'=\mathrm{u}'\mathrm{x}+\mathrm{u} \\ $$$$\mathrm{y}'=\frac{\mathrm{x}^{\mathrm{3}} \mathrm{u}^{\mathrm{2}} +\mathrm{2x}^{\mathrm{3}} \mathrm{u}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{3}} \mathrm{u}+\mathrm{x}^{\mathrm{3}} \mathrm{u}^{\mathrm{2}} }=\mathrm{u}'\mathrm{x}+\mathrm{u} \\ $$$$\Rightarrow\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{2u}^{\mathrm{3}} }{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{2}} }−\mathrm{u}=\mathrm{u}'\mathrm{x} \\ $$$$\Rightarrow\frac{\mathrm{u}^{\mathrm{3}} −\mathrm{u}}{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{2}} }=\frac{\mathrm{du}}{\mathrm{dx}}\mathrm{x} \\ $$$$\Rightarrow\frac{\mathrm{dx}}{\mathrm{x}}=\frac{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{3}} −\mathrm{u}}\mathrm{du} \\ $$$$\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{C}=\int\frac{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{3}} −\mathrm{u}}\mathrm{du}=\int\frac{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{2}} }{\mathrm{u}\left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{1}\right)}\mathrm{du} \\ $$$$\mathrm{use}\:\mathrm{partial}\:\mathrm{fractions}: \\ $$$$\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{C}=−\int\frac{\mathrm{du}}{\mathrm{u}}+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{du}}{\mathrm{u}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{du}}{\mathrm{u}+\mathrm{1}} \\ $$$$=−\mathrm{ln}\left(\mathrm{u}\right)+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{u}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{u}+\mathrm{1}\right) \\ $$$$=−\mathrm{ln}\left(\mathrm{u}\right)+\mathrm{ln}\sqrt{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{3}} }+\mathrm{ln}\sqrt{\mathrm{u}+\mathrm{1}} \\ $$$$=\mathrm{ln}\left(\frac{\sqrt{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{u}+\mathrm{1}\right)}}{\mathrm{u}}\right)=\mathrm{lnx}+\mathrm{C} \\ $$$$\Rightarrow\frac{\sqrt{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{u}+\mathrm{1}\right)}}{\mathrm{u}}=\mathrm{Cx} \\ $$$$\frac{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{u}+\mathrm{1}\right)}{\mathrm{u}^{\mathrm{2}} }=\mathrm{C}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{u}^{\mathrm{4}} −\mathrm{2u}^{\mathrm{3}} −\mathrm{Cx}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} +\mathrm{2u}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{u}\therefore\mathrm{y}=\mathrm{ux} \\ $$$$\mathrm{note}\:\mathrm{that}\:\mathrm{if}\:\mathrm{C}=\mathrm{0}\Rightarrow\mathrm{u}=\pm\mathrm{1} \\ $$$$\mathrm{y}=\pm\mathrm{x}\:\mathrm{which}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *