Question Number 119002 by benjo_mathlover last updated on 21/Oct/20
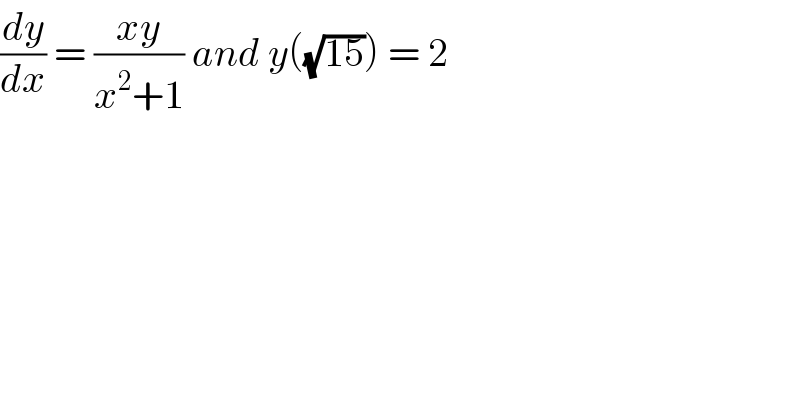
$$\frac{{dy}}{{dx}}\:=\:\frac{{xy}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{and}\:{y}\left(\sqrt{\mathrm{15}}\right)\:=\:\mathrm{2} \\ $$
Answered by bramlexs22 last updated on 21/Oct/20
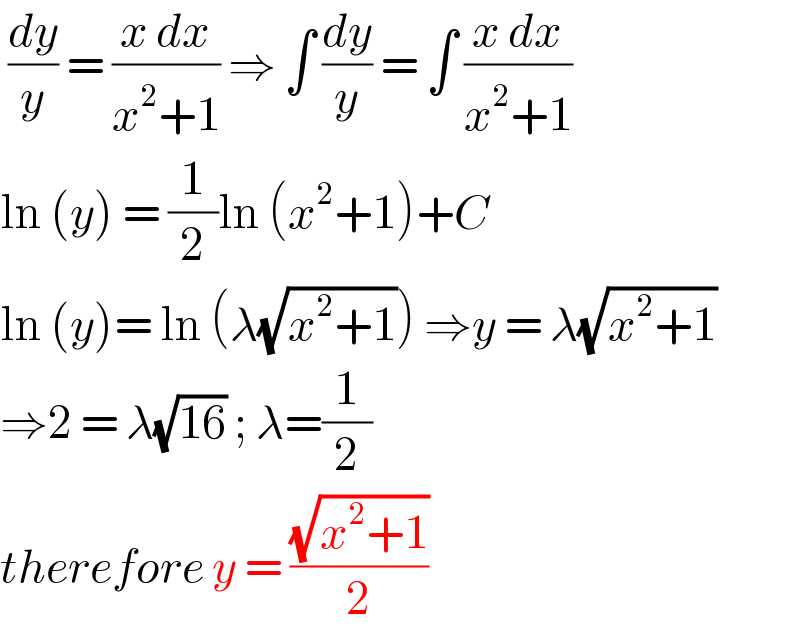
$$\:\frac{{dy}}{{y}}\:=\:\frac{{x}\:{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\:\int\:\frac{{dy}}{{y}}\:=\:\int\:\frac{{x}\:{dx}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{ln}\:\left({y}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{C}\: \\ $$$$\mathrm{ln}\:\left({y}\right)=\:\mathrm{ln}\:\left(\lambda\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\:\Rightarrow{y}\:=\:\lambda\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}\:=\:\lambda\sqrt{\mathrm{16}}\:;\:\lambda=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${therefore}\:{y}\:=\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}} \\ $$
