Question Number 181613 by Mastermind last updated on 27/Nov/22
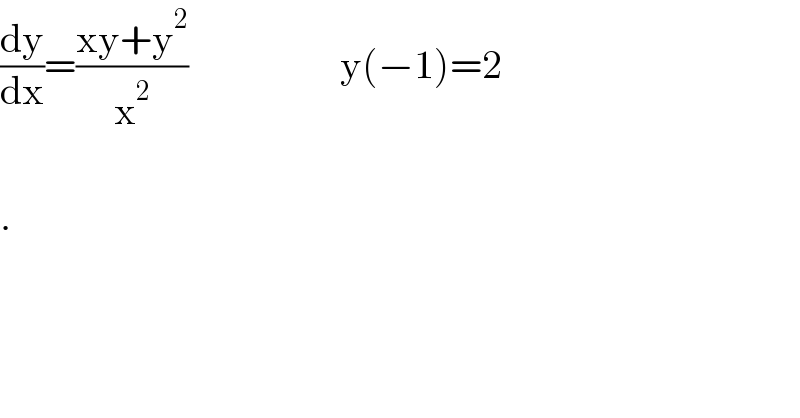
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\left(−\mathrm{1}\right)=\mathrm{2} \\ $$$$ \\ $$$$. \\ $$
Answered by FelipeLz last updated on 27/Nov/22
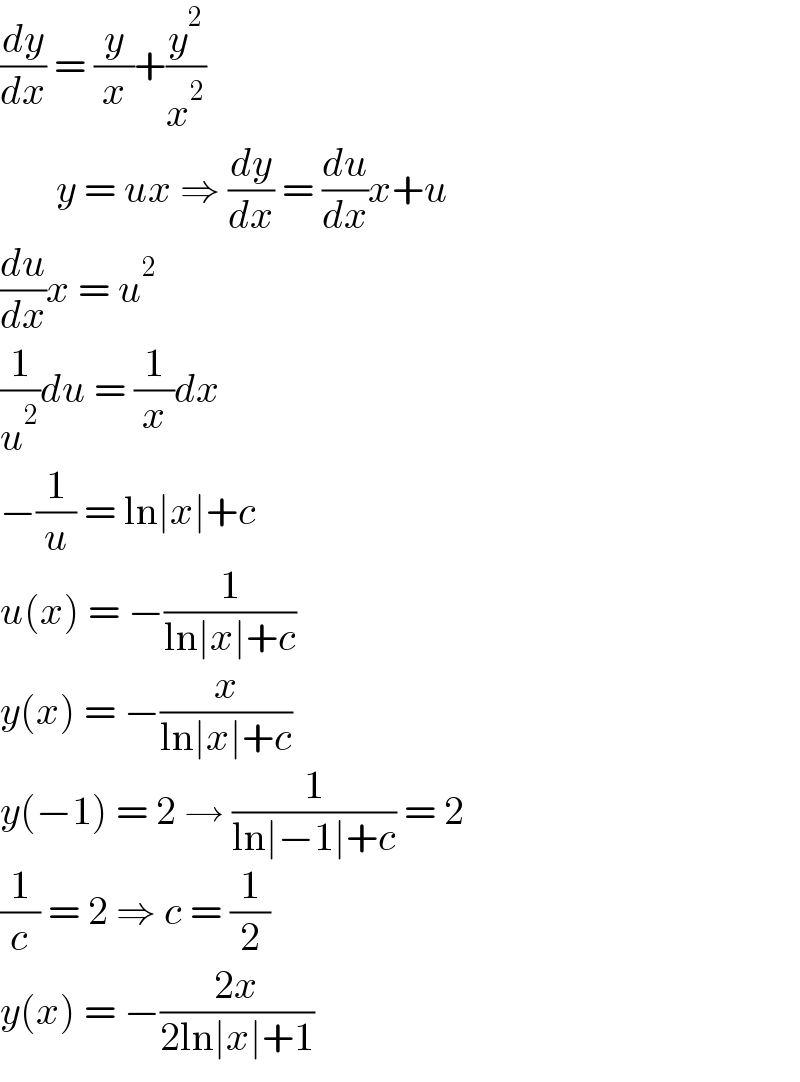
$$\frac{{dy}}{{dx}}\:=\:\frac{{y}}{{x}}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\:\:{y}\:=\:{ux}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{{du}}{{dx}}{x}+{u} \\ $$$$\frac{{du}}{{dx}}{x}\:=\:{u}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{u}^{\mathrm{2}} }{du}\:=\:\frac{\mathrm{1}}{{x}}{dx} \\ $$$$−\frac{\mathrm{1}}{{u}}\:=\:\mathrm{ln}\mid{x}\mid+{c} \\ $$$${u}\left({x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{ln}\mid{x}\mid+{c}} \\ $$$${y}\left({x}\right)\:=\:−\frac{{x}}{\mathrm{ln}\mid{x}\mid+{c}} \\ $$$${y}\left(−\mathrm{1}\right)\:=\:\mathrm{2}\:\rightarrow\:\frac{\mathrm{1}}{\mathrm{ln}\mid−\mathrm{1}\mid+{c}}\:=\:\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{c}}\:=\:\mathrm{2}\:\Rightarrow\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}\left({x}\right)\:=\:−\frac{\mathrm{2}{x}}{\mathrm{2ln}\mid{x}\mid+\mathrm{1}}\: \\ $$
