Question Number 89809 by jagoll last updated on 19/Apr/20

$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{xy}−\mathrm{x}^{\mathrm{2}} } \\ $$
Answered by john santu last updated on 19/Apr/20
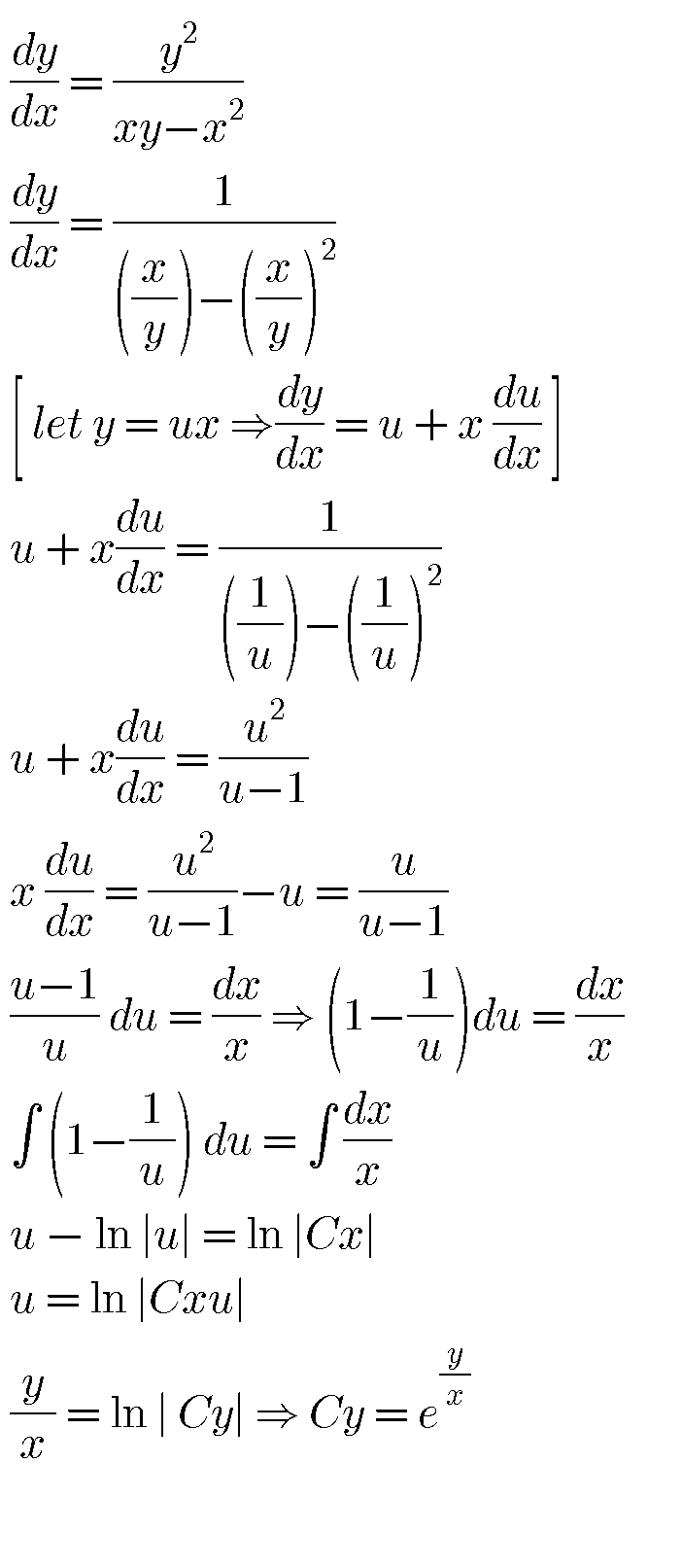
Answered by mr W last updated on 19/Apr/20
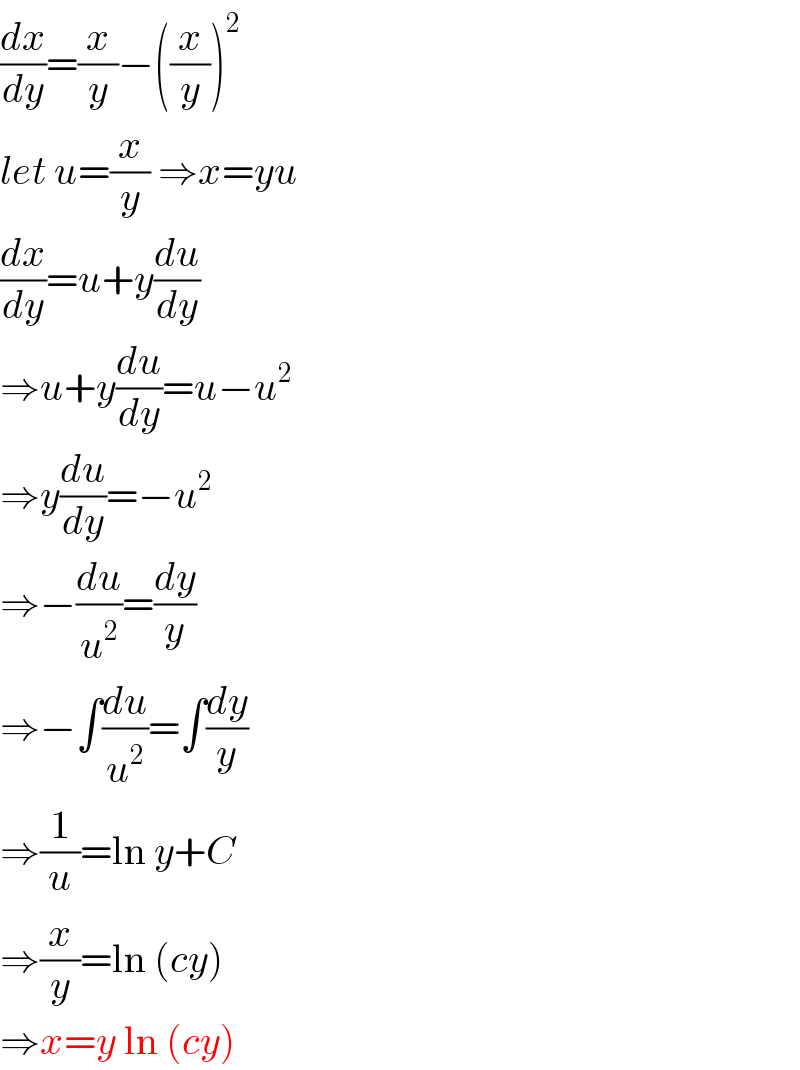
$$\frac{{dx}}{{dy}}=\frac{{x}}{{y}}−\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} \\ $$$${let}\:{u}=\frac{{x}}{{y}}\:\Rightarrow{x}={yu} \\ $$$$\frac{{dx}}{{dy}}={u}+{y}\frac{{du}}{{dy}} \\ $$$$\Rightarrow{u}+{y}\frac{{du}}{{dy}}={u}−{u}^{\mathrm{2}} \\ $$$$\Rightarrow{y}\frac{{du}}{{dy}}=−{u}^{\mathrm{2}} \\ $$$$\Rightarrow−\frac{{du}}{{u}^{\mathrm{2}} }=\frac{{dy}}{{y}} \\ $$$$\Rightarrow−\int\frac{{du}}{{u}^{\mathrm{2}} }=\int\frac{{dy}}{{y}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{u}}=\mathrm{ln}\:{y}+{C} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\mathrm{ln}\:\left({cy}\right) \\ $$$$\Rightarrow{x}={y}\:\mathrm{ln}\:\left({cy}\right) \\ $$
Answered by 242242864 last updated on 19/Apr/20
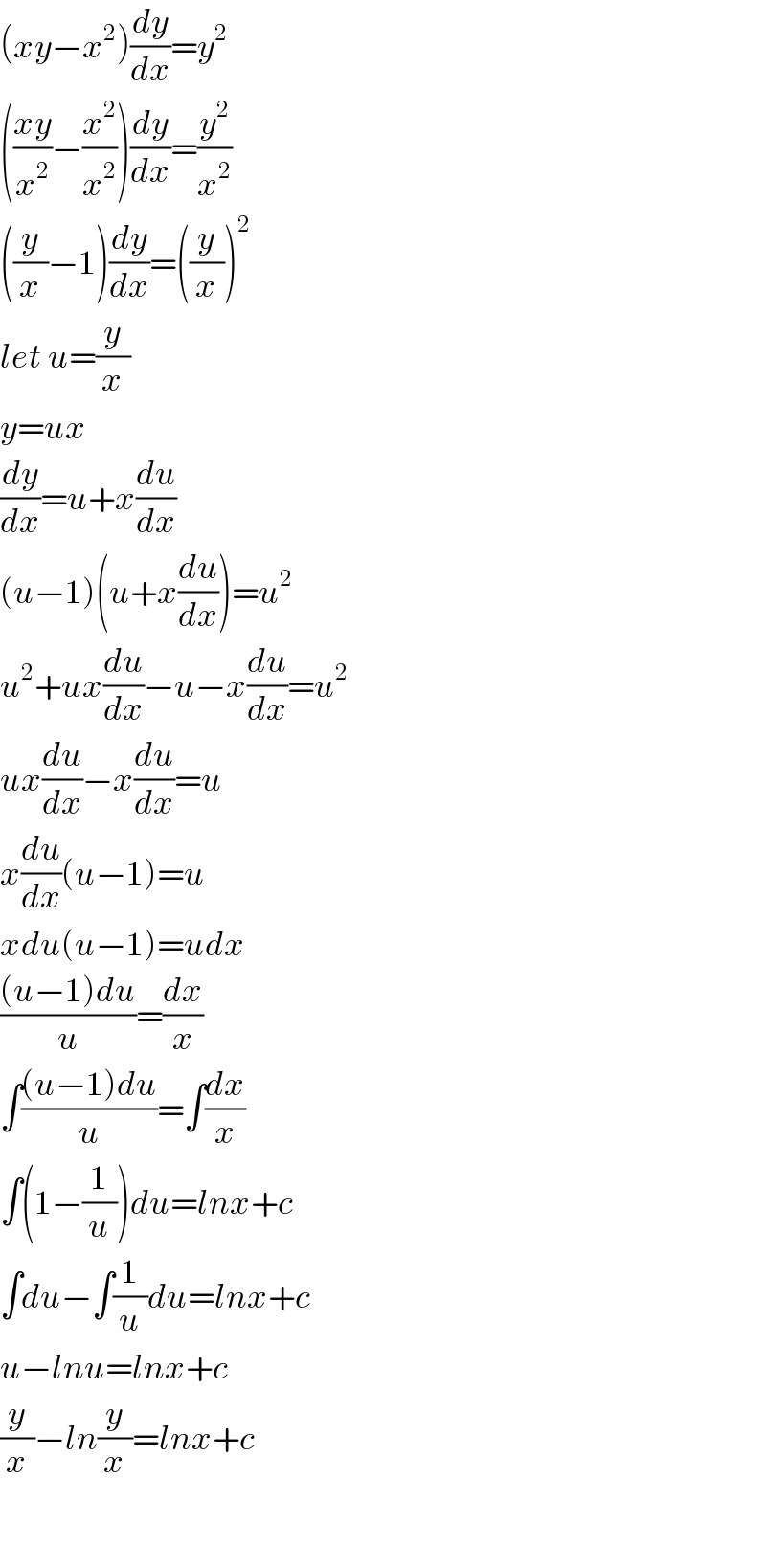
$$\left({xy}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}={y}^{\mathrm{2}} \\ $$$$\left(\frac{{xy}}{{x}^{\mathrm{2}} }−\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)\frac{{dy}}{{dx}}=\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$\left(\frac{{y}}{{x}}−\mathrm{1}\right)\frac{{dy}}{{dx}}=\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \\ $$$${let}\:{u}=\frac{{y}}{{x}} \\ $$$${y}={ux} \\ $$$$\frac{{dy}}{{dx}}={u}+{x}\frac{{du}}{{dx}} \\ $$$$\left({u}−\mathrm{1}\right)\left({u}+{x}\frac{{du}}{{dx}}\right)={u}^{\mathrm{2}} \\ $$$${u}^{\mathrm{2}} +{ux}\frac{{du}}{{dx}}−{u}−{x}\frac{{du}}{{dx}}={u}^{\mathrm{2}} \\ $$$${ux}\frac{{du}}{{dx}}−{x}\frac{{du}}{{dx}}={u} \\ $$$${x}\frac{{du}}{{dx}}\left({u}−\mathrm{1}\right)={u} \\ $$$${xdu}\left({u}−\mathrm{1}\right)={udx} \\ $$$$\frac{\left({u}−\mathrm{1}\right){du}}{{u}}=\frac{{dx}}{{x}} \\ $$$$\int\frac{\left({u}−\mathrm{1}\right){du}}{{u}}=\int\frac{{dx}}{{x}} \\ $$$$\int\left(\mathrm{1}−\frac{\mathrm{1}}{{u}}\right){du}={lnx}+{c} \\ $$$$\int{du}−\int\frac{\mathrm{1}}{{u}}{du}={lnx}+{c} \\ $$$${u}−{lnu}={lnx}+{c} \\ $$$$\frac{{y}}{{x}}−{ln}\frac{{y}}{{x}}={lnx}+{c} \\ $$$$ \\ $$
