Question Number 156855 by cortano last updated on 16/Oct/21
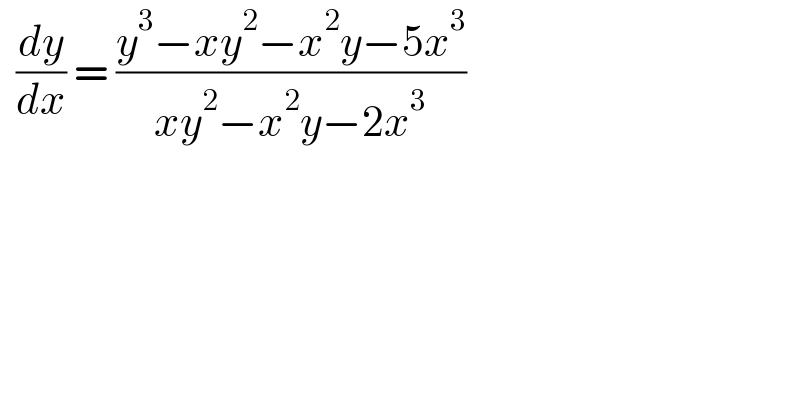
$$\:\:\frac{{dy}}{{dx}}\:=\:\frac{{y}^{\mathrm{3}} −{xy}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}−\mathrm{5}{x}^{\mathrm{3}} }{{xy}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}−\mathrm{2}{x}^{\mathrm{3}} }\: \\ $$$$\: \\ $$
Answered by gsk2684 last updated on 27/Oct/21
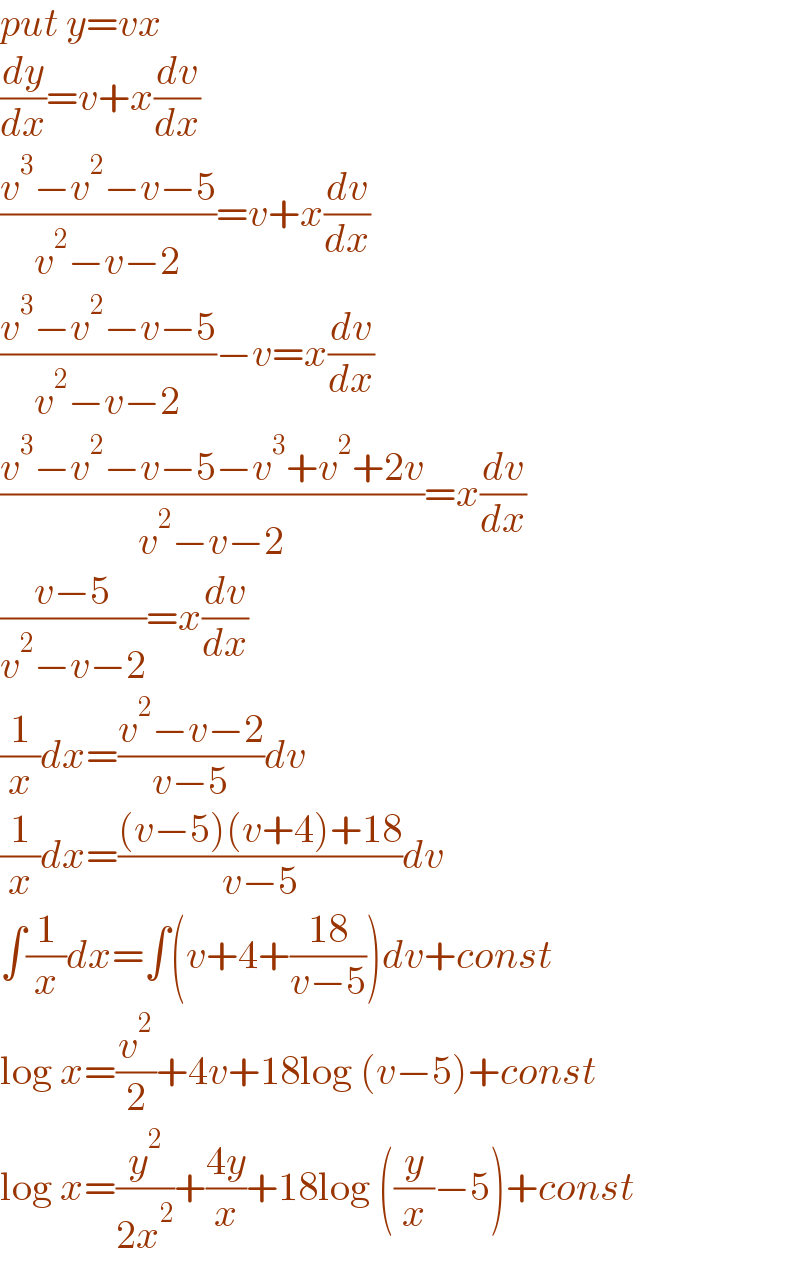
$${put}\:{y}={vx} \\ $$$$\frac{{dy}}{{dx}}={v}+{x}\frac{{dv}}{{dx}} \\ $$$$\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} −{v}−\mathrm{5}}{{v}^{\mathrm{2}} −{v}−\mathrm{2}}={v}+{x}\frac{{dv}}{{dx}} \\ $$$$\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} −{v}−\mathrm{5}}{{v}^{\mathrm{2}} −{v}−\mathrm{2}}−{v}={x}\frac{{dv}}{{dx}} \\ $$$$\frac{{v}^{\mathrm{3}} −{v}^{\mathrm{2}} −{v}−\mathrm{5}−{v}^{\mathrm{3}} +{v}^{\mathrm{2}} +\mathrm{2}{v}}{{v}^{\mathrm{2}} −{v}−\mathrm{2}}={x}\frac{{dv}}{{dx}} \\ $$$$\frac{{v}−\mathrm{5}}{{v}^{\mathrm{2}} −{v}−\mathrm{2}}={x}\frac{{dv}}{{dx}} \\ $$$$\frac{\mathrm{1}}{{x}}{dx}=\frac{{v}^{\mathrm{2}} −{v}−\mathrm{2}}{{v}−\mathrm{5}}{dv} \\ $$$$\frac{\mathrm{1}}{{x}}{dx}=\frac{\left({v}−\mathrm{5}\right)\left({v}+\mathrm{4}\right)+\mathrm{18}}{{v}−\mathrm{5}}{dv} \\ $$$$\int\frac{\mathrm{1}}{{x}}{dx}=\int\left({v}+\mathrm{4}+\frac{\mathrm{18}}{{v}−\mathrm{5}}\right){dv}+{const} \\ $$$$\mathrm{log}\:{x}=\frac{{v}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{4}{v}+\mathrm{18log}\:\left({v}−\mathrm{5}\right)+{const} \\ $$$$\mathrm{log}\:{x}=\frac{{y}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{4}{y}}{{x}}+\mathrm{18log}\:\left(\frac{{y}}{{x}}−\mathrm{5}\right)+{const} \\ $$
Commented by cortano last updated on 16/Oct/21

$${yes} \\ $$
