Question Number 83028 by jagoll last updated on 27/Feb/20
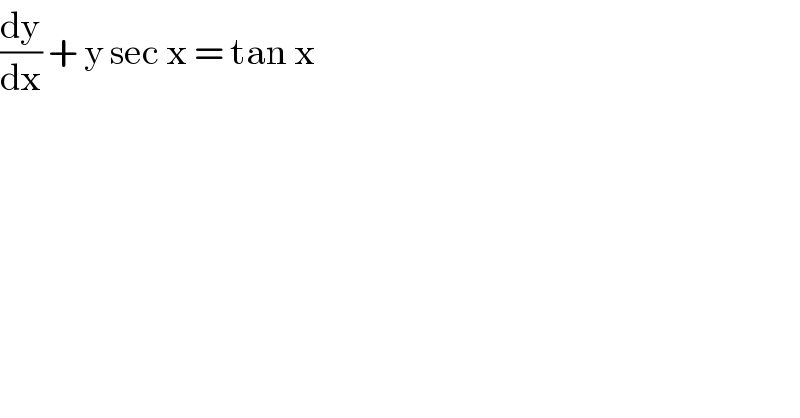
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\mathrm{y}\:\mathrm{sec}\:\mathrm{x}\:=\:\mathrm{tan}\:\mathrm{x} \\ $$
Commented by john santu last updated on 27/Feb/20
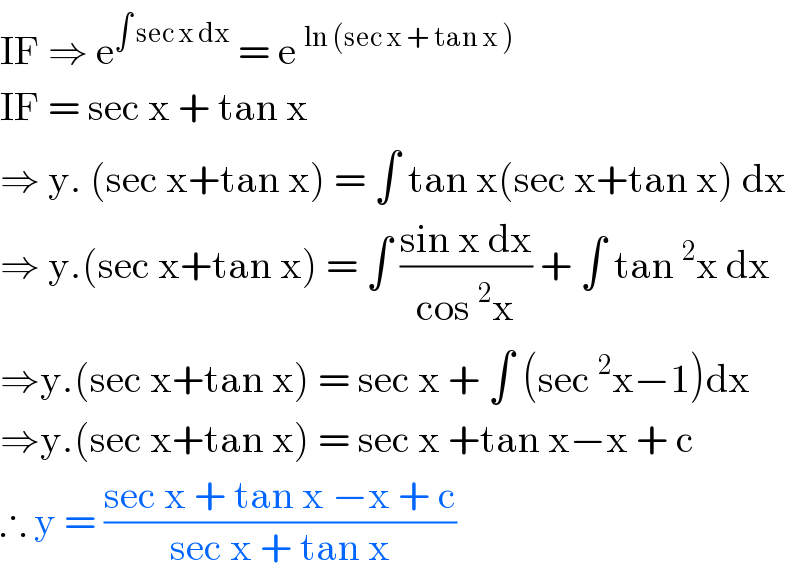
$$\mathrm{IF}\:\Rightarrow\:\mathrm{e}^{\int\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}} \:=\:\mathrm{e}\:^{\mathrm{ln}\:\left(\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\:\right)\:} \\ $$$$\mathrm{IF}\:=\:\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\: \\ $$$$\Rightarrow\:\mathrm{y}.\:\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:=\:\int\:\mathrm{tan}\:\mathrm{x}\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:\mathrm{dx} \\ $$$$\Rightarrow\:\mathrm{y}.\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:=\:\int\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:+\:\int\:\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$\Rightarrow\mathrm{y}.\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:=\:\mathrm{sec}\:\mathrm{x}\:+\:\int\:\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\Rightarrow\mathrm{y}.\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:=\:\mathrm{sec}\:\mathrm{x}\:+\mathrm{tan}\:\mathrm{x}−\mathrm{x}\:+\:\mathrm{c} \\ $$$$\therefore\:\mathrm{y}\:=\:\frac{\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}\:−\mathrm{x}\:+\:\mathrm{c}}{\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}} \\ $$
Commented by jagoll last updated on 27/Feb/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by john santu last updated on 27/Feb/20

$$\mathrm{ok} \\ $$
