dy-dx-y-sinx-

Question Number 104265 by mohammad17 last updated on 20/Jul/20

\frac{d y}{d x} - y = s i n x

Answered by bemath last updated on 20/Jul/20

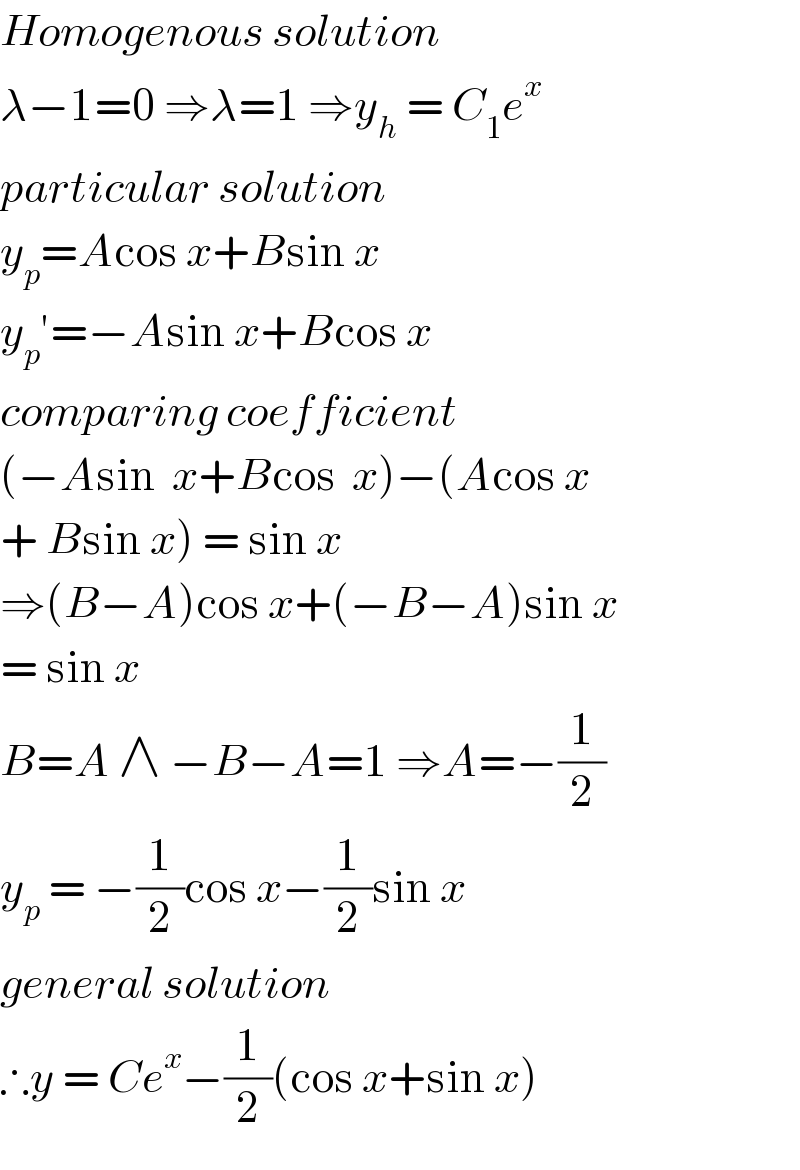
H o m o g e n o u s s o l u t i o n

λ - 1 = 0 \Rightarrow λ = 1 \Rightarrow y_{h} = C_{1} e^{x}

p a r t i c u l a r s o l u t i o n

y_{p} = A \cos x + B \sin x

y_{p}^{'} = - A \sin x + B \cos x

c o m p a r i n g c o e f f i c i e n t

(- A \sin x + B \cos x) - (A \cos x

+ B \sin x) = \sin x

\Rightarrow (B - A) \cos x + (- B - A) \sin x

= \sin x

B = A \land - B - A = 1 \Rightarrow A = - \frac{1}{2}

y_{p} = - \frac{1}{2} \cos x - \frac{1}{2} \sin x

g e n e r a l s o l u t i o n

∴ y = {C e}^{x} - \frac{1}{2} (\cos x + \sin x)

Commented by mohammad17 last updated on 20/Jul/20

s o r y s i r h o w t h i s i t h i n k t h i s y = \frac{\int e^{- x} s i n x d x}{e^{- x}}

Commented by mohammad17 last updated on 20/Jul/20

Commented by mohammad17 last updated on 20/Jul/20

i s t h e s o l u t i o n i t s r i g h t ?

Commented by bemath last updated on 20/Jul/20

y e s s i r

Commented by mohammad17 last updated on 20/Jul/20

t h a n k y o u

Answered by Dwaipayan Shikari last updated on 20/Jul/20

IF = e^{\int - 1 dx} = e^{- x}

y . e^{- x} = \int e^{- x} sinxdx = I

{ye}^{- x} = - {sinxe}^{- x} + \int e^{- x} cosxdx

{ye}^{- x} = - sinx e^{- x} - cosx e^{- x} - \int sinx e^{- x} = I

{ye}^{- x} = - \frac{1}{2} e^{- x} (sinx + cosx) + C

y = \frac{- 1}{2} (sinx + cosx) + {Ce}^{x}

Answered by Ar Brandon last updated on 20/Jul/20

{\frac{dy}{dx} - y = sinx} \cdot e^{- x}

\Rightarrow e^{- x} \frac{dy}{dx} - {ye}^{- x} = e^{- x} sinx

\Rightarrow \frac{d ({ye}^{- x})}{dx} = e^{- x} sinx

\Rightarrow {ye}^{- x} = \int e^{- x} sinxdx

= sinx \int e^{- x} dx - \int {\frac{dsinx}{dx} \int e^{- x} dx} dx

= - e^{- x} sinx + \int e^{- x} cosxdx

= - e^{- x} sinx + {cosx \int e^{- x} dx - \int {\frac{dcosx}{dx} \int e^{- x} dx} dx}

= - e^{- x} sinx - e^{- x} cosx - \int e^{- x} sinxdx

= \frac{- (sinx + cosx) e^{- x}}{2} + C

\Rightarrow y = - \frac{(sinx + cosx)}{2} + C e^{x}

Answered by mathmax by abdo last updated on 20/Jul/20

y^{^{'}} - y = sinx

h \to r - 1 = 0 \Rightarrow r = 1 \Rightarrow y_{h} = {Ke}^{x}

lagrange method \to y^{^{'}} = k^{^{'}} e^{x} + {ke}^{x}

e \Rightarrow k^{^{'}} e^{x} + {ke}^{x} - {ke}^{x} = sinx \Rightarrow k^{^{'}} = e^{- x} sinx \Rightarrow k = \int e^{- x} sinx dx

= Im (\int e^{- x + ix} dx) = Im (\int e^{(- 1 + i) x} dx) but

\int e^{(- 1 + i) x} dx = \frac{1}{- 1 + i} e^{(- 1 + i) x} + c = - \frac{1}{1 - i} e^{- x} (cosx + sinx)

= - \frac{1 + i}{2} e^{- x} {cosx + isinx} = - \frac{e^{- x}}{2} {cosx + isinx + icosx - sinx} \Rightarrow

Im (\int \dots) = - \frac{e^{- x}}{2} {cosx + sinx} \Rightarrow the general solution is

(- \frac{e^{- x}}{2} {cosx + sinx} + c) e^{x} = - \frac{1}{2} (cosx + sinx) + {ce}^{x}