Question Number 89600 by jagoll last updated on 18/Apr/20
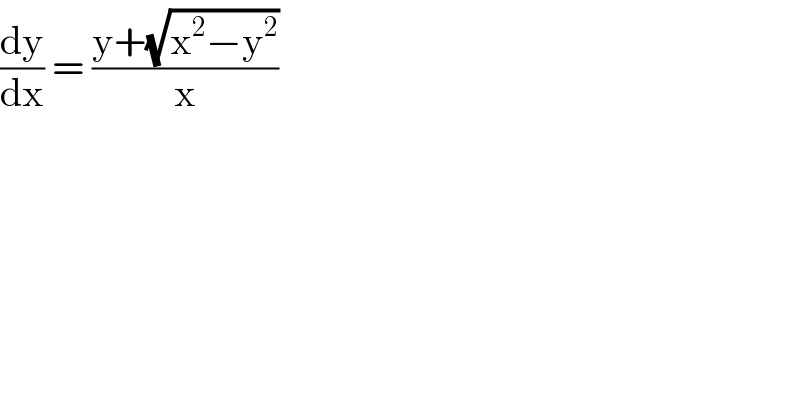
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{y}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}{\mathrm{x}}\: \\ $$
Commented by mr W last updated on 18/Apr/20
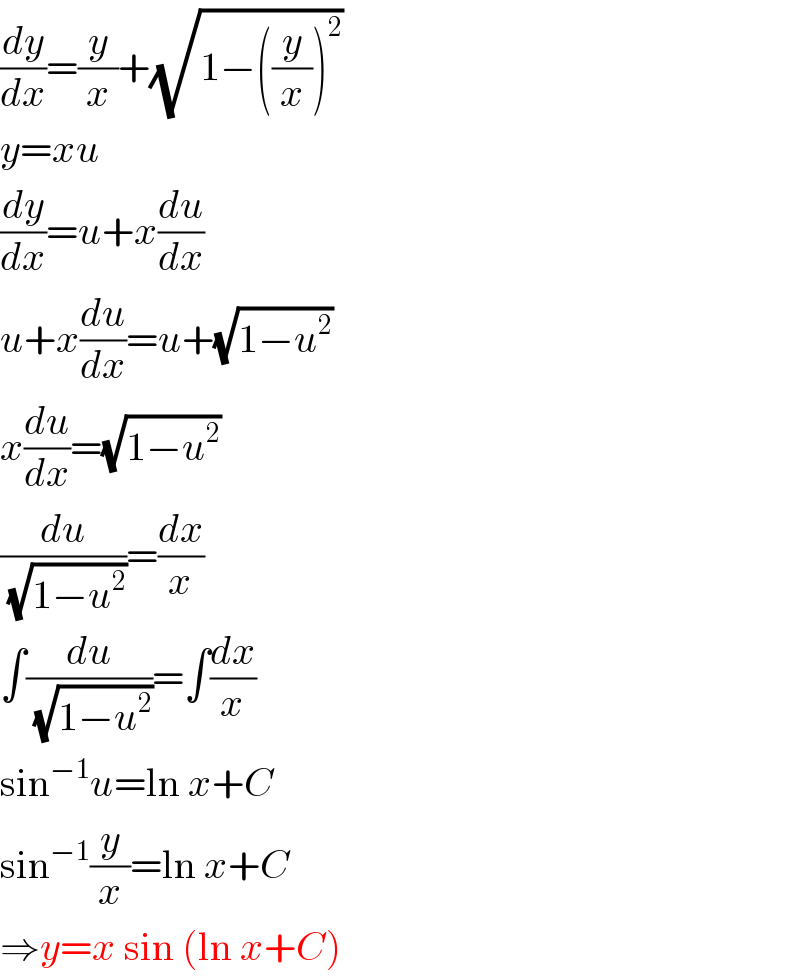
$$\frac{{dy}}{{dx}}=\frac{{y}}{{x}}+\sqrt{\mathrm{1}−\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} } \\ $$$${y}={xu} \\ $$$$\frac{{dy}}{{dx}}={u}+{x}\frac{{du}}{{dx}} \\ $$$${u}+{x}\frac{{du}}{{dx}}={u}+\sqrt{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$${x}\frac{{du}}{{dx}}=\sqrt{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}=\frac{{dx}}{{x}} \\ $$$$\int\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}=\int\frac{{dx}}{{x}} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {u}=\mathrm{ln}\:{x}+{C} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \frac{{y}}{{x}}=\mathrm{ln}\:{x}+{C} \\ $$$$\Rightarrow{y}={x}\:\mathrm{sin}\:\left(\mathrm{ln}\:{x}+{C}\right) \\ $$
Commented by jagoll last updated on 18/Apr/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
