Question Number 129126 by benjo_mathlover last updated on 13/Jan/21
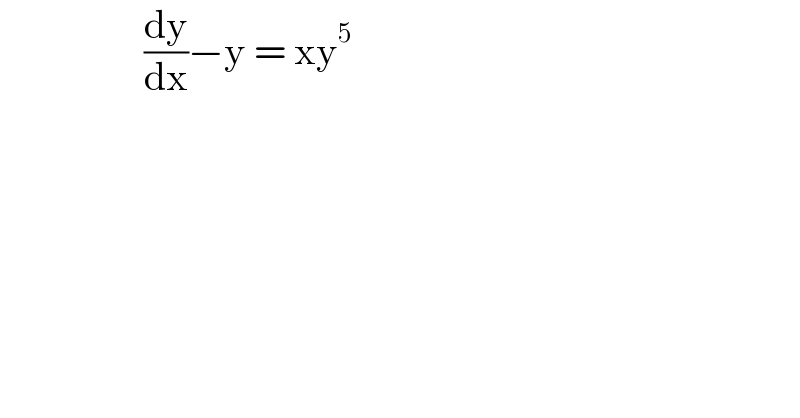
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{y}\:=\:\mathrm{xy}^{\mathrm{5}} \: \\ $$
Answered by liberty last updated on 13/Jan/21
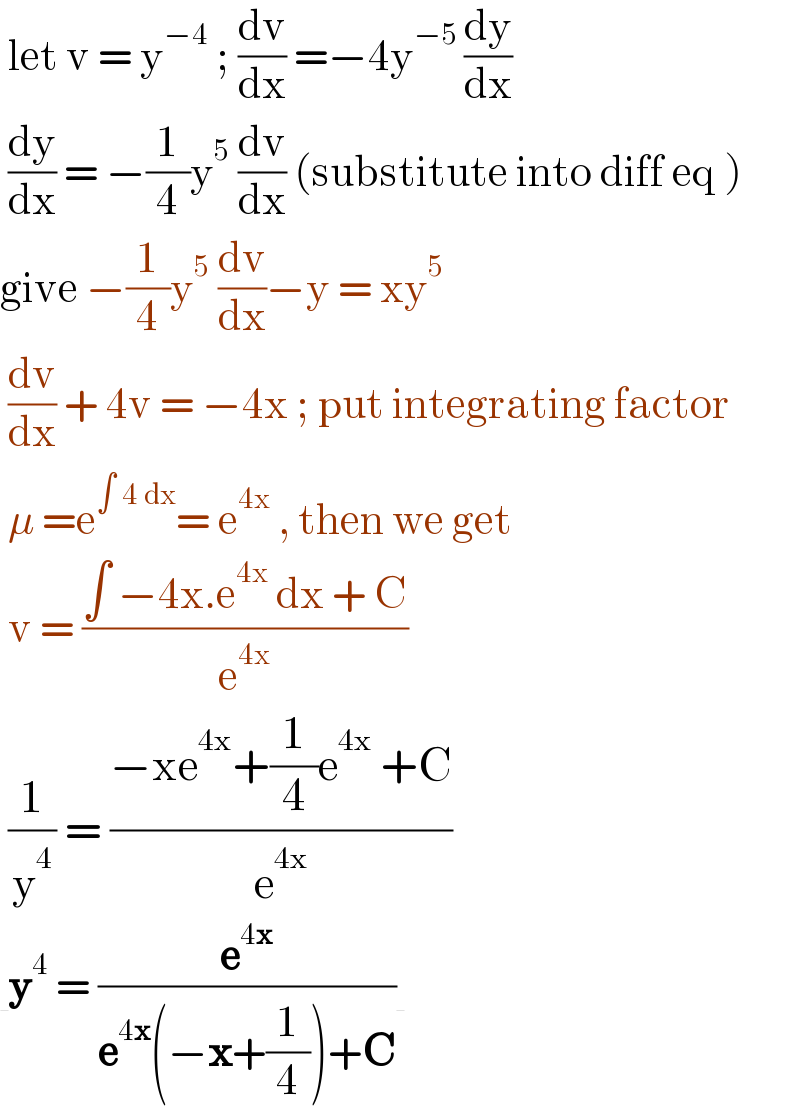
$$\:\mathrm{let}\:\mathrm{v}\:=\:\mathrm{y}^{−\mathrm{4}} \:;\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=−\mathrm{4y}^{−\mathrm{5}\:} \frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{y}^{\mathrm{5}} \:\frac{\mathrm{dv}}{\mathrm{dx}}\:\left(\mathrm{substitute}\:\mathrm{into}\:\mathrm{diff}\:\mathrm{eq}\:\right) \\ $$$$\mathrm{give}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{y}^{\mathrm{5}} \:\frac{\mathrm{dv}}{\mathrm{dx}}−\mathrm{y}\:=\:\mathrm{xy}^{\mathrm{5}} \\ $$$$\:\frac{\mathrm{dv}}{\mathrm{dx}}\:+\:\mathrm{4v}\:=\:−\mathrm{4x}\:;\:\mathrm{put}\:\mathrm{integrating}\:\mathrm{factor} \\ $$$$\:\mu\:=\mathrm{e}^{\int\:\mathrm{4}\:\mathrm{dx}} =\:\mathrm{e}^{\mathrm{4x}} \:,\:\mathrm{then}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\:\mathrm{v}\:=\:\frac{\int\:−\mathrm{4x}.\mathrm{e}^{\mathrm{4x}} \:\mathrm{dx}\:+\:\mathrm{C}}{\mathrm{e}^{\mathrm{4x}} } \\ $$$$\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{4}} }\:=\:\frac{−\mathrm{xe}^{\mathrm{4x}} +\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{4x}} \:+\mathrm{C}}{\mathrm{e}^{\mathrm{4x}} } \\ $$$$\underline{\:}\boldsymbol{\mathrm{y}}^{\mathrm{4}} \:=\:\frac{\boldsymbol{\mathrm{e}}^{\mathrm{4}\boldsymbol{\mathrm{x}}} }{\boldsymbol{\mathrm{e}}^{\mathrm{4}\boldsymbol{\mathrm{x}}} \left(−\boldsymbol{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\boldsymbol{\mathrm{C}}}\underline{\:}\:\: \\ $$
