Question Number 87461 by hamdhan last updated on 04/Apr/20
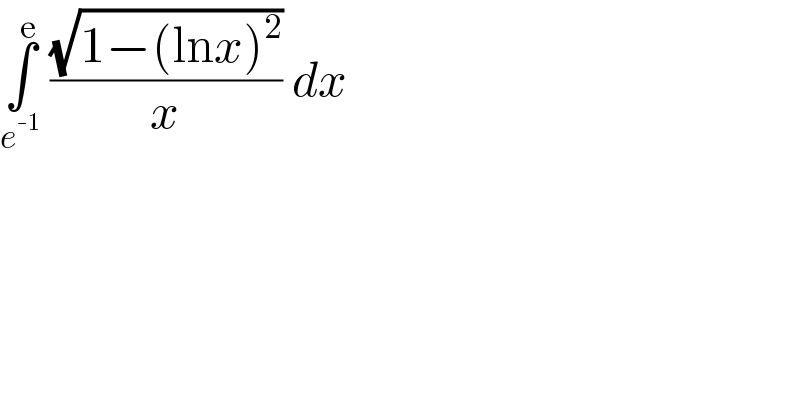
$$\underset{{e}^{-\mathrm{1}} } {\overset{\mathrm{e}} {\int}}\:\frac{\sqrt{\mathrm{1}−\left(\mathrm{ln}{x}\right)^{\mathrm{2}} }}{{x}}\:{dx} \\ $$
Commented by ajfour last updated on 04/Apr/20
![let ln x=t ⇒ (dx)/x=dt I=2∫_0 ^( 1) (√(1−t^2 )) dt = [t(√(1−t^2 ))+sin^(−1) t ]_0 ^1 = π/2 .](https://www.tinkutara.com/question/Q87463.png)
$${let}\:\:\mathrm{ln}\:{x}={t}\:\:\:\:\Rightarrow\:\:\left({dx}\right)/{x}={dt} \\ $$$${I}=\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt} \\ $$$$\:\:=\:\left[{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }+\mathrm{sin}^{−\mathrm{1}} {t}\:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:=\:\pi/\mathrm{2}\:. \\ $$
Answered by Ar Brandon last updated on 04/Apr/20
![Let x=e^y ⇒dx=e^y dy I=∫_(−1) ^1 ((√(1−y^2 ))/e^y )∙e^y dy= ∫_(−1) ^1 (√(1−y^2 ))dy I=(√(1−y^2 ))∫_(−1) ^1 dy−∫_(−1) ^1 [(d/dy)((√(1−y^2 )))∫dy]dy =[y(√(1−y^2 ))]_(−1) ^1 +∫_(−1) ^1 [(y^2 /( (√(1−y^2 ))))]dy let y=sin θ ⇒dy=cos θdθ I=∫_(−(π/2)) ^(π/2) sin^2 θ dθ=(1/2)∫_(−(π/2)) ^(π/2) (1−cos(2θ))dθ I=(1/2)[θ−(1/2)sin(2θ)]_(−(π/2)) ^(π/2) I=(1/2)[(π/2)+(π/2)]=(π/2)](https://www.tinkutara.com/question/Q87465.png)
$$\boldsymbol{{Let}}\:\:\boldsymbol{{x}}=\boldsymbol{{e}}^{\boldsymbol{{y}}} \:\:\Rightarrow\boldsymbol{{dx}}=\boldsymbol{{e}}^{\boldsymbol{{y}}} \boldsymbol{{dy}} \\ $$$$\boldsymbol{{I}}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }}{\boldsymbol{{e}}^{\boldsymbol{{y}}} }\centerdot\boldsymbol{{e}}^{\boldsymbol{{y}}} \boldsymbol{{dy}}=\:\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\mathrm{1}−\boldsymbol{{y}}^{\mathrm{2}} }\boldsymbol{{dy}} \\ $$$${I}=\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\int_{−\mathrm{1}} ^{\mathrm{1}} {dy}−\int_{−\mathrm{1}} ^{\mathrm{1}} \left[\frac{{d}}{{dy}}\left(\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\right)\int{dy}\right]{dy} \\ $$$$\:\:=\left[{y}\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }\right]_{−\mathrm{1}} ^{\mathrm{1}} +\int_{−\mathrm{1}} ^{\mathrm{1}} \left[\frac{{y}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}\right]{dy} \\ $$$$\:\:{let}\:{y}={sin}\:\theta\:\Rightarrow{dy}={cos}\:\theta{d}\theta \\ $$$${I}=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} \theta\:{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left[\theta−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right]=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
