Question Number 85360 by sahnaz last updated on 21/Mar/20
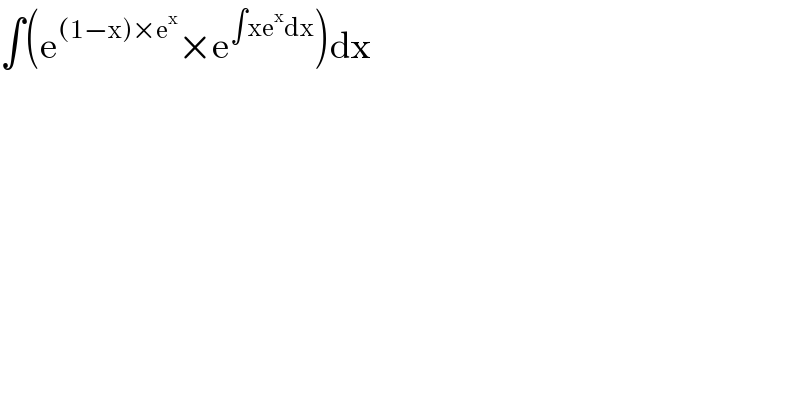
$$\int\left(\mathrm{e}^{\left(\mathrm{1}−\mathrm{x}\right)×\mathrm{e}^{\mathrm{x}} } ×\mathrm{e}^{\int\mathrm{xe}^{\mathrm{x}} \mathrm{dx}} \right)\mathrm{dx} \\ $$
Answered by john santu last updated on 21/Mar/20
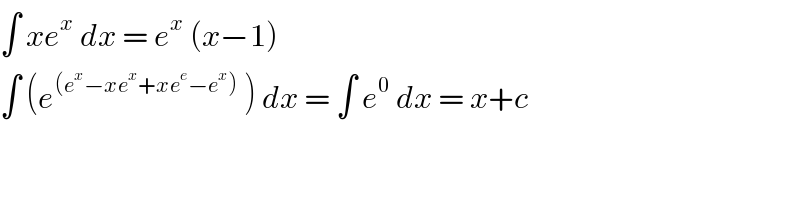
$$\int\:{xe}^{{x}} \:{dx}\:=\:{e}^{{x}} \:\left({x}−\mathrm{1}\right)\: \\ $$$$\int\:\left({e}^{\left({e}^{{x}} −{xe}^{{x}} +{xe}^{{e}} −{e}^{{x}} \right)} \:\right)\:{dx}\:=\:\int\:{e}^{\mathrm{0}} \:{dx}\:=\:{x}+{c} \\ $$
