Question Number 84879 by sahnaz last updated on 17/Mar/20

$$\mathrm{e}^{\int\frac{\mathrm{2dx}}{\mathrm{xlnx}}} \\ $$
Commented by jagoll last updated on 17/Mar/20
![∫ ((2dx)/(x lnx)) = ∫ ((2d(lnx))/(lnx)) = ∫ 2(du/u) = 2 ln u + c , [u = ln x ] = 2ln(lnx) + 2lnC = 2ln(Clnx) e^(∫ ((2dx)/(lnx))) = e^([ln(Clnx )^2 ]) = (Cln x)^2](https://www.tinkutara.com/question/Q84880.png)
$$\int\:\frac{\mathrm{2dx}}{\mathrm{x}\:\mathrm{lnx}}\:=\:\int\:\frac{\mathrm{2d}\left(\mathrm{lnx}\right)}{\mathrm{lnx}}\:=\:\int\:\mathrm{2}\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=\:\mathrm{2}\:\mathrm{ln}\:\mathrm{u}\:+\:\mathrm{c}\:,\:\left[\mathrm{u}\:=\:\mathrm{ln}\:\mathrm{x}\:\right] \\ $$$$=\:\mathrm{2ln}\left(\mathrm{lnx}\right)\:+\:\mathrm{2lnC}\:=\:\mathrm{2ln}\left(\mathrm{Clnx}\right) \\ $$$$\mathrm{e}^{\int\:\frac{\mathrm{2dx}}{\mathrm{lnx}}} \:=\:\mathrm{e}^{\left[\mathrm{ln}\left(\mathrm{Clnx}\:\right)^{\mathrm{2}} \:\right]} \:=\:\left(\mathrm{Cln}\:\mathrm{x}\right)^{\mathrm{2}} \\ $$
Answered by bshahid010@gmail.com last updated on 17/Mar/20
![∫_e ^2 (dx/(x.lnx)) put lnx=t⇒(1/x)dx=dt ∫_e ^2 (dt/t)⇒[lnt]_e ^2 =[ln(lnx)]_e ^2 =ln(ln(2))−ln(ln(e)) ln(ln(2))](https://www.tinkutara.com/question/Q84883.png)
$$\underset{\mathrm{e}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{dx}}{\mathrm{x}.\mathrm{lnx}}\:\mathrm{put}\:\mathrm{lnx}=\mathrm{t}\Rightarrow\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}=\mathrm{dt} \\ $$$$\underset{\mathrm{e}} {\overset{\mathrm{2}} {\int}}\frac{\mathrm{dt}}{\mathrm{t}}\Rightarrow\left[\mathrm{lnt}\underset{\mathrm{e}} {\overset{\mathrm{2}} {\right]}}=\left[\mathrm{ln}\left(\mathrm{lnx}\right)\underset{\mathrm{e}} {\overset{\mathrm{2}} {\right]}}=\mathrm{ln}\left(\mathrm{ln}\left(\mathrm{2}\right)\right)−\mathrm{ln}\left(\mathrm{ln}\left(\mathrm{e}\right)\right) \\ $$$$\mathrm{ln}\left(\mathrm{ln}\left(\mathrm{2}\right)\right) \\ $$$$ \\ $$$$ \\ $$
Commented by john santu last updated on 17/Mar/20

$$\mathrm{the}\:\mathrm{question}\:\mathrm{e}\:^{\int\:\frac{\mathrm{2dx}}{\mathrm{x}\:\mathrm{ln}\:\mathrm{x}}} \:\mathrm{sir} \\ $$
Answered by bshahid010@gmail.com last updated on 18/Mar/20
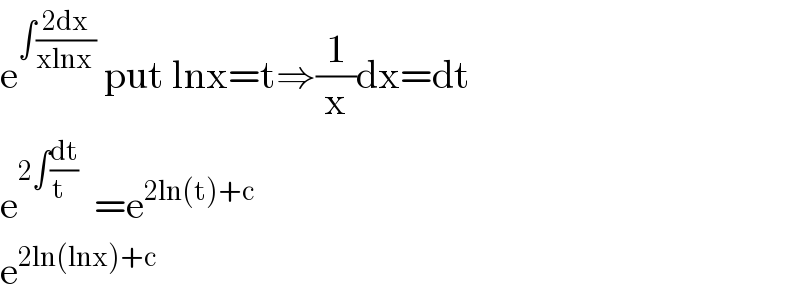
$$\mathrm{e}^{\int\frac{\mathrm{2dx}}{\mathrm{xlnx}\:}} \:\mathrm{put}\:\mathrm{lnx}=\mathrm{t}\Rightarrow\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx}=\mathrm{dt} \\ $$$$\mathrm{e}^{\mathrm{2}\int\frac{\mathrm{dt}}{\mathrm{t}\:\:\:}} \:\:=\mathrm{e}^{\mathrm{2ln}\left(\mathrm{t}\right)+\mathrm{c}} \:\:\:\: \\ $$$$\mathrm{e}^{\mathrm{2ln}\left(\mathrm{lnx}\right)+\mathrm{c}} \\ $$
