Question Number 156080 by SANOGO last updated on 07/Oct/21
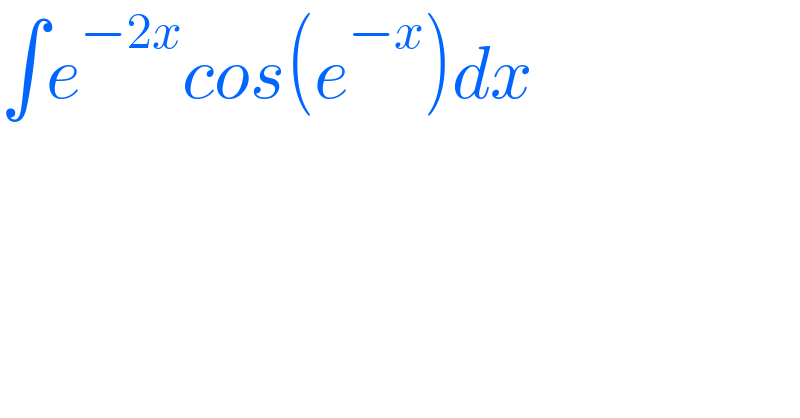
$$\int{e}^{−\mathrm{2}{x}} {cos}\left({e}^{−{x}} \right){dx} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 07/Oct/21
![u=e^(−x) ⇒ du=−e^(−x) dx= I=∫e^(−x) cos(e^(−x) )∙e^(−x) dx =−∫ucos(u)du=−[usinx+cosx]+C](https://www.tinkutara.com/question/Q156084.png)
$${u}={e}^{−{x}} \Rightarrow\:{du}=−{e}^{−{x}} {dx}= \\ $$$${I}=\int{e}^{−{x}} \mathrm{cos}\left({e}^{−{x}} \right)\centerdot{e}^{−{x}} {dx} \\ $$$$\:\:=−\int{u}\mathrm{cos}\left({u}\right){du}=−\left[{u}\mathrm{sin}{x}+\mathrm{cos}{x}\right]+{C} \\ $$
