Question Number 106809 by Study last updated on 07/Aug/20

$$\int{e}^{\mathrm{2}{x}} {sine}^{{x}} {dx}=?? \\ $$
Answered by bemath last updated on 07/Aug/20
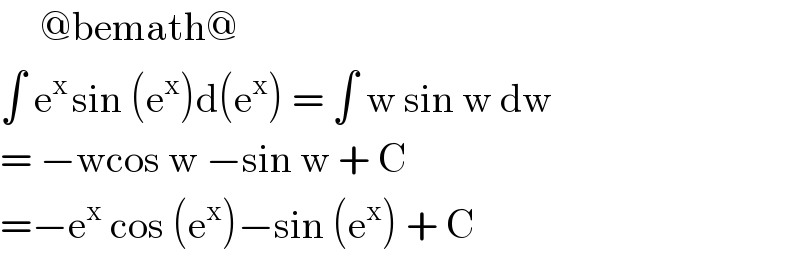
$$\:\:\:\:\:@\mathrm{bemath}@ \\ $$$$\int\:\mathrm{e}^{\mathrm{x}\:} \mathrm{sin}\:\left(\mathrm{e}^{\mathrm{x}} \right)\mathrm{d}\left(\mathrm{e}^{\mathrm{x}} \right)\:=\:\int\:\mathrm{w}\:\mathrm{sin}\:\mathrm{w}\:\mathrm{dw} \\ $$$$=\:−\mathrm{wcos}\:\mathrm{w}\:−\mathrm{sin}\:\mathrm{w}\:+\:\mathrm{C} \\ $$$$=−\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}\:\left(\mathrm{e}^{\mathrm{x}} \right)−\mathrm{sin}\:\left(\mathrm{e}^{\mathrm{x}} \right)\:+\:\mathrm{C}\: \\ $$
Commented by malwaan last updated on 07/Aug/20
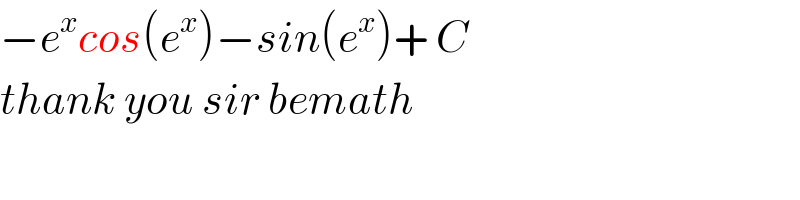
$$−{e}^{{x}} {cos}\left({e}^{{x}} \right)−{sin}\left({e}^{{x}} \right)+\:{C} \\ $$$${thank}\:{you}\:{sir}\:{bemath} \\ $$
Commented by bemath last updated on 07/Aug/20
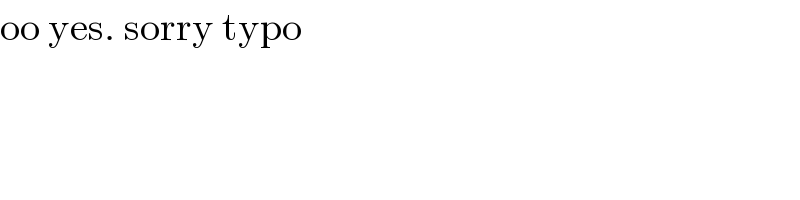
$$\mathrm{oo}\:\mathrm{yes}.\:\mathrm{sorry}\:\mathrm{typo} \\ $$
Answered by mathmax by abdo last updated on 07/Aug/20
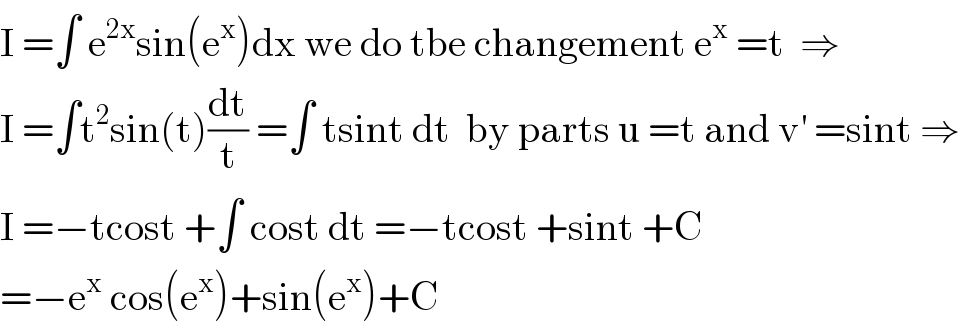
$$\mathrm{I}\:=\int\:\mathrm{e}^{\mathrm{2x}} \mathrm{sin}\left(\mathrm{e}^{\mathrm{x}} \right)\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{x}} \:=\mathrm{t}\:\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\mathrm{t}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{t}\right)\frac{\mathrm{dt}}{\mathrm{t}}\:=\int\:\mathrm{tsint}\:\mathrm{dt}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}\:=\mathrm{t}\:\mathrm{and}\:\mathrm{v}^{'} \:=\mathrm{sint}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\mathrm{tcost}\:+\int\:\mathrm{cost}\:\mathrm{dt}\:=−\mathrm{tcost}\:+\mathrm{sint}\:+\mathrm{C} \\ $$$$=−\mathrm{e}^{\mathrm{x}} \:\mathrm{cos}\left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{sin}\left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{C} \\ $$
