Question Number 35202 by Cheyboy last updated on 16/May/18
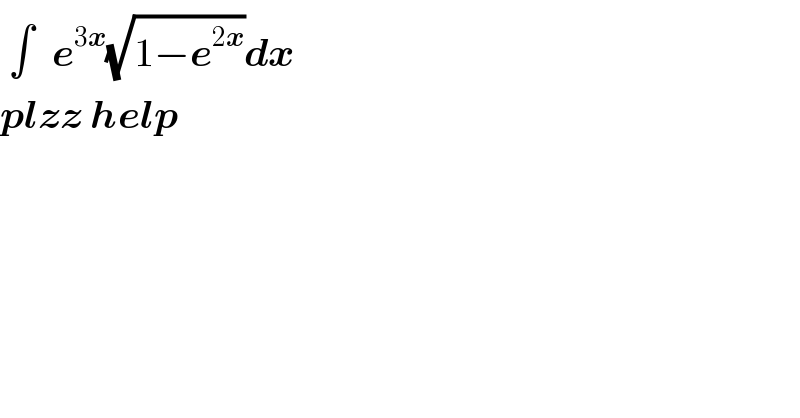
$$\:\int^{} \:\boldsymbol{{e}}^{\mathrm{3}\boldsymbol{{x}}} \sqrt{\mathrm{1}−\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} }\boldsymbol{{dx}} \\ $$$$\boldsymbol{{plzz}}\:\boldsymbol{{help}} \\ $$
Answered by ajfour last updated on 16/May/18
![let e^x =t ⇒ e^x dx = dt I=∫e^(2x) (√(1−e^(2x) )) e^x dx =∫t^2 (√(1−t^2 )) dt now let t=sin θ ⇒ dt=cos θdθ I=∫sin^2 θcos^2 θdθ =(1/8)∫(1−cos 4θ)dθ =(θ/8)−((sin 4θ)/(32))+c =((sin^(−1) (e^x ))/8)−(1/(32))sin [4sin^(−1) (e^x )]+c .](https://www.tinkutara.com/question/Q35204.png)
$${let}\:{e}^{{x}} ={t}\:\:\:\Rightarrow\:\:{e}^{{x}} {dx}\:=\:{dt} \\ $$$${I}=\int{e}^{\mathrm{2}{x}} \sqrt{\mathrm{1}−{e}^{\mathrm{2}{x}} }\:{e}^{{x}} {dx}\:=\int{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt} \\ $$$${now}\:{let}\:\:{t}=\mathrm{sin}\:\theta\:\:\Rightarrow\:\:{dt}=\mathrm{cos}\:\theta{d}\theta \\ $$$${I}=\int\mathrm{sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{1}−\mathrm{cos}\:\mathrm{4}\theta\right){d}\theta \\ $$$$\:\:\:=\frac{\theta}{\mathrm{8}}−\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{32}}+{c} \\ $$$$\:\:\:=\frac{\mathrm{sin}^{−\mathrm{1}} \left({e}^{{x}} \right)}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\:\left[\mathrm{4sin}^{−\mathrm{1}} \left({e}^{{x}} \right)\right]+{c}\:\:. \\ $$
Commented by Cheyboy last updated on 16/May/18

$$\mathscr{T}{hankx}\:{alot}\:{sir} \\ $$
