Question Number 51420 by Tawa1 last updated on 26/Dec/18
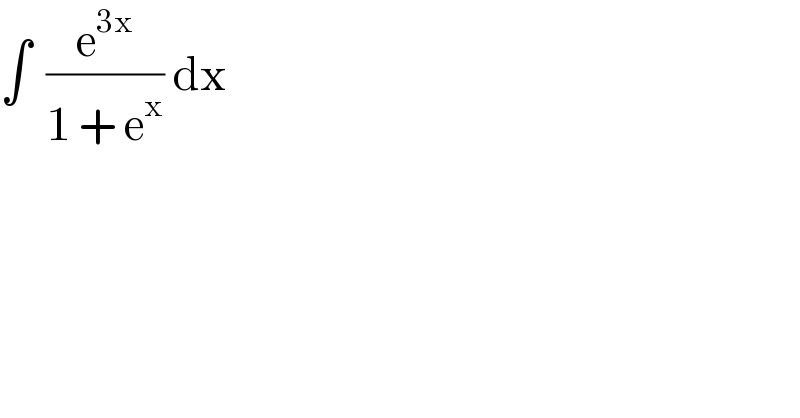
$$\int\:\:\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{1}\:+\:\mathrm{e}^{\mathrm{x}} }\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 26/Dec/18
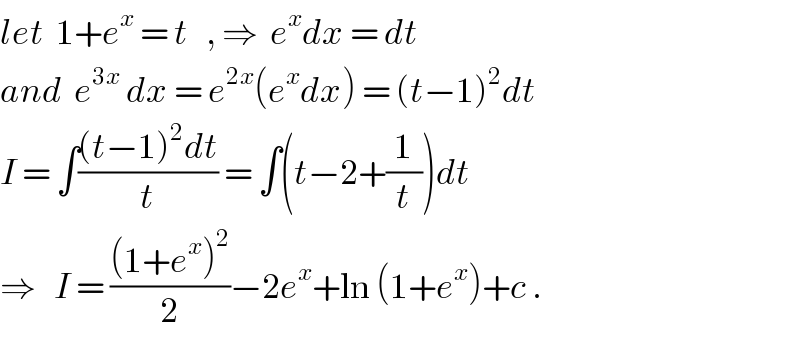
$${let}\:\:\mathrm{1}+{e}^{{x}} \:=\:{t}\:\:\:,\:\Rightarrow\:\:{e}^{{x}} {dx}\:=\:{dt} \\ $$$${and}\:\:{e}^{\mathrm{3}{x}} \:{dx}\:=\:{e}^{\mathrm{2}{x}} \left({e}^{{x}} {dx}\right)\:=\:\left({t}−\mathrm{1}\right)^{\mathrm{2}} {dt} \\ $$$${I}\:=\:\int\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {dt}}{{t}}\:=\:\int\left({t}−\mathrm{2}+\frac{\mathrm{1}}{{t}}\right){dt} \\ $$$$\Rightarrow\:\:\:{I}\:=\:\frac{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{e}^{{x}} +\mathrm{ln}\:\left(\mathrm{1}+{e}^{{x}} \right)+{c}\:. \\ $$
Commented by Tawa1 last updated on 26/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Smail last updated on 26/Dec/18
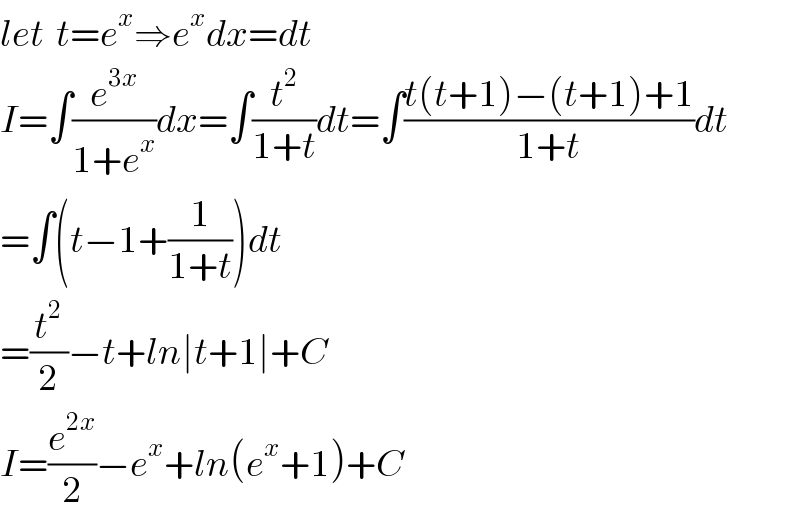
$${let}\:\:{t}={e}^{{x}} \Rightarrow{e}^{{x}} {dx}={dt} \\ $$$${I}=\int\frac{{e}^{\mathrm{3}{x}} }{\mathrm{1}+{e}^{{x}} }{dx}=\int\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}}{dt}=\int\frac{{t}\left({t}+\mathrm{1}\right)−\left({t}+\mathrm{1}\right)+\mathrm{1}}{\mathrm{1}+{t}}{dt} \\ $$$$=\int\left({t}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−{t}+{ln}\mid{t}+\mathrm{1}\mid+{C} \\ $$$${I}=\frac{{e}^{\mathrm{2}{x}} }{\mathrm{2}}−{e}^{{x}} +{ln}\left({e}^{{x}} +\mathrm{1}\right)+{C} \\ $$
Commented by Tawa1 last updated on 26/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
