Question Number 102043 by Dwaipayan Shikari last updated on 06/Jul/20

$$\int{e}^{\sqrt{{ax}+{b}}} {dx} \\ $$
Commented by Dwaipayan Shikari last updated on 06/Jul/20
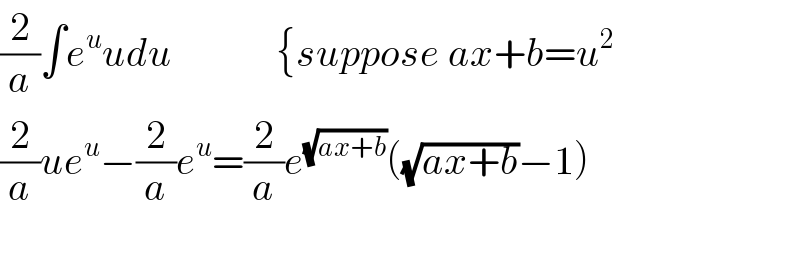
$$\frac{\mathrm{2}}{{a}}\int{e}^{{u}} {udu}\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{{suppose}\:{ax}+{b}={u}^{\mathrm{2}} \right. \\ $$$$\frac{\mathrm{2}}{{a}}{ue}^{{u}} −\frac{\mathrm{2}}{{a}}{e}^{{u}} =\frac{\mathrm{2}}{{a}}{e}^{\sqrt{{ax}+{b}}} \left(\sqrt{{ax}+{b}}−\mathrm{1}\right) \\ $$$$ \\ $$
