Question Number 110490 by ManojMaity last updated on 29/Aug/20

$$ \\ $$$${e}^{\mathrm{i}\pi} \:=\:−\mathrm{1} \\ $$
Answered by nimnim last updated on 29/Aug/20
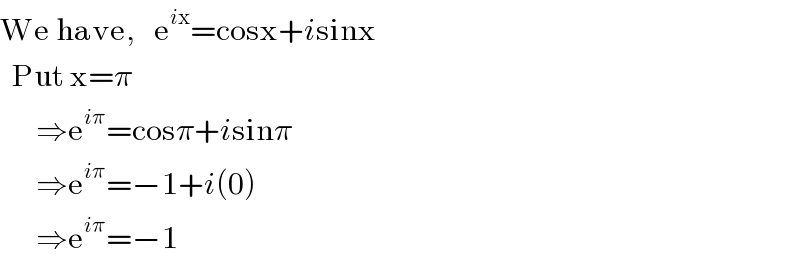
$$\mathrm{We}\:\mathrm{have},\:\:\:\mathrm{e}^{{i}\mathrm{x}} =\mathrm{cosx}+{i}\mathrm{sinx}\: \\ $$$$\:\:\mathrm{Put}\:\mathrm{x}=\pi \\ $$$$\:\:\:\:\:\:\Rightarrow\mathrm{e}^{{i}\pi} =\mathrm{cos}\pi+{i}\mathrm{sin}\pi \\ $$$$\:\:\:\:\:\:\Rightarrow\mathrm{e}^{{i}\pi} =−\mathrm{1}+{i}\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\Rightarrow\mathrm{e}^{{i}\pi} =−\mathrm{1} \\ $$
