e-ipi-1-squaring-both-sides-e-2pii-1-e-0-comparing-powers-2pii-0-pi-0-or-i-0-

Question Number 33473 by 33 last updated on 17/Apr/18

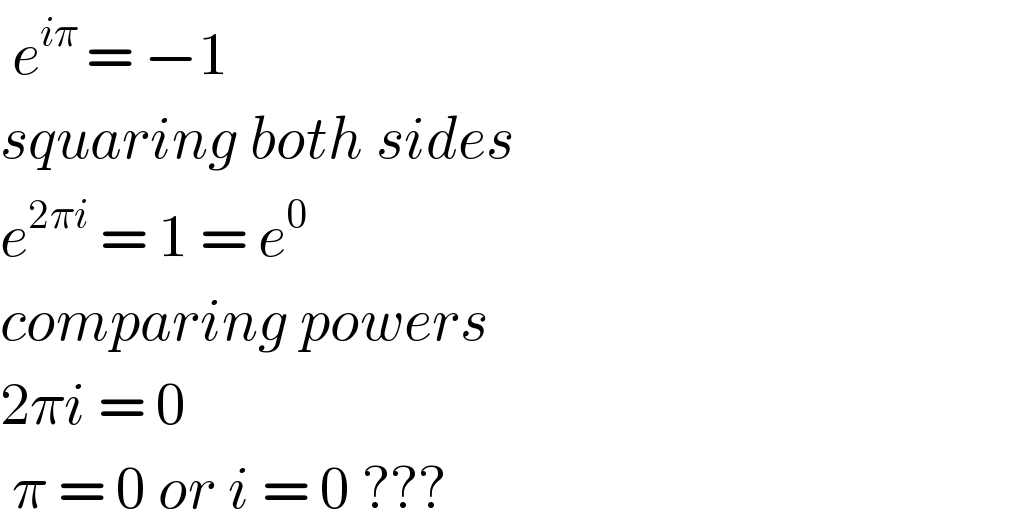
e^{i π} = - 1

s q u a r i n g b o t h s i d e s

e^{2 π i} = 1 = e^{0}

c o m p a r i n g p o w e r s

2 π i = 0

π = 0 o r i = 0 ? ? ?

Commented by abdo imad last updated on 17/Apr/18

l o o k s i r t h e f o n c t i o n R \to] 0, + \infty [/ f (x) = e^{x} i s a b i j e c t i o n

f r o m R t o] 0, + \infty [f o r t h a t w e h a v e e^{x} = e^{y} \Leftrightarrow x = y

b u t t h e f u n c t i o n R \to C / g (x) = e^{i x} i s n o t a b i j e c t i o n a n d

e^{i x} = e^{i y} \Leftrightarrow x = y + 2 k π w i t h k \in Z a n d i f z = r e^{i θ}, r > 0

l n (z) = l n r + i (θ + 2 k π) b u t w e t a k e o n l y

l n (z) = l n r + i θ a s a p r i n c i p a l d e t e r m i n a t i o n o f t h e

c o m p l e x l o g a r i t h m e .

Commented by Joel578 last updated on 17/Apr/18

Same like \sin π = \sin 0

then π = 0 ? ?

Or {(- 1)}^{2} = 1^{2}

then - 1 = 1 ? ?

Guess why {it}^{'} s incorrect

Commented by 33 last updated on 17/Apr/18

b u t s i r,

{(- 1)}^{2} = 1^{2} ⇏ - 1 = 1

y o u a r e t a k i n g s q r o o t h e r e

w h i c h i s n o t v a l i d .

i d i d n o t t a k e s q u a r e r o o t .

A n d s i n e i s a

m a n y o n e f u n c t i o n .

f (x) = f (x + a)

⇏ x = x + a

f o r m a n y o n e f u n c t i o n s .

b u t e^{x} i s o n e o n e .

h e n c e e^{x} = e^{y} m u s t i m p l y

x = y

Answered by MJS last updated on 17/Apr/18

you {can}^{'} t compare the powers

in this case, because e^{φ i} is a

periodic function

z = a + b i = r (\cos φ + i \sin φ) = {r e}^{φ i}

[with r = abs (z) = \sqrt{a^{2} + b^{2}}

and φ = \tan^{- 1} \frac{b}{a}]

because \sin φ and \cos φ are periodic

it should be clear that for n \in N_{0}

z = r (\cos (φ \pm 2 n π) + i \sin (φ \pm 2 n π)) \Rightarrow

\Rightarrow z = {r e}^{φ \pm 2 n π}

therefore, e^{0} = e^{2 π i} ⇏ 0 = 2 π i

but you made another mistake :

x^{y} = - 1 ∣^{2}

x^{2 y} = 1

x^{2 y} = x^{0}

2 y = 0

y = 0

BUT x^{0} \neq - 1

\Rightarrow squaring both sides might

lead to wrong results

Commented by 33 last updated on 17/Apr/18

h a h a v e r y a p t e x p l a n a t i o n

s i r . t h a n k s f o r y o u r

e f f o r t .

Facebook Tweet Pin