Question Number 128347 by mathocean1 last updated on 06/Jan/21
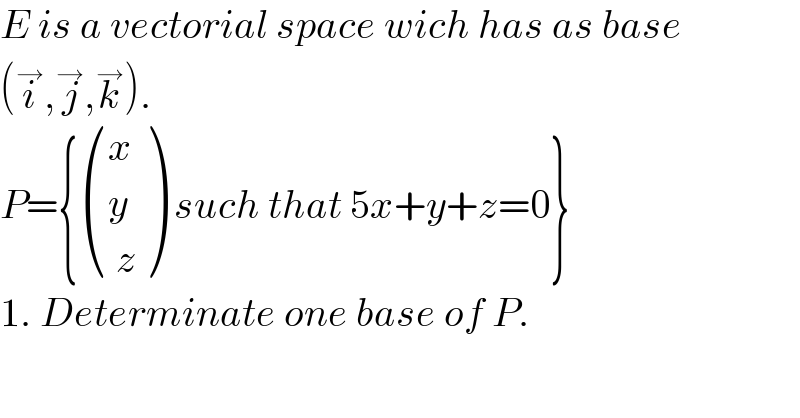
$${E}\:{is}\:{a}\:{vectorial}\:{space}\:{wich}\:{has}\:{as}\:{base}\: \\ $$$$\left(\overset{\rightarrow} {{i}},\overset{\rightarrow} {{j}},\overset{\rightarrow} {{k}}\right).\: \\ $$$${P}=\left\{\begin{pmatrix}{{x}}\\{{y}}\\{\:{z}}\end{pmatrix}\:{such}\:{that}\:\mathrm{5}{x}+{y}+{z}=\mathrm{0}\right\} \\ $$$$\mathrm{1}.\:{Determinate}\:{one}\:{base}\:{of}\:{P}. \\ $$
