Question Number 13412 by tawa tawa last updated on 19/May/17
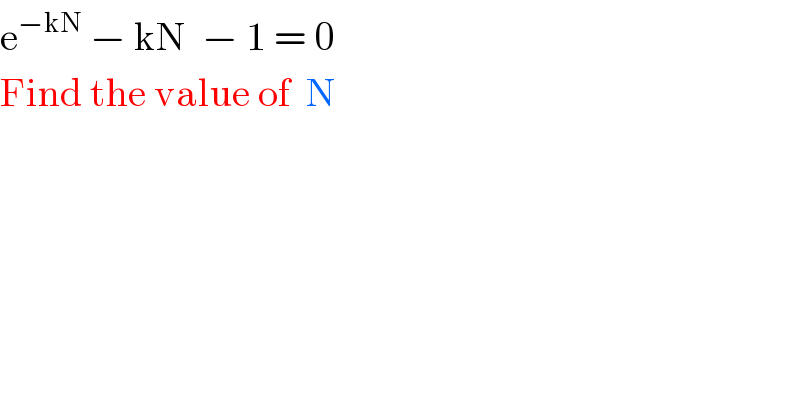
$$\mathrm{e}^{−\mathrm{kN}} \:−\:\mathrm{kN}\:\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{N} \\ $$
Answered by mrW1 last updated on 20/May/17
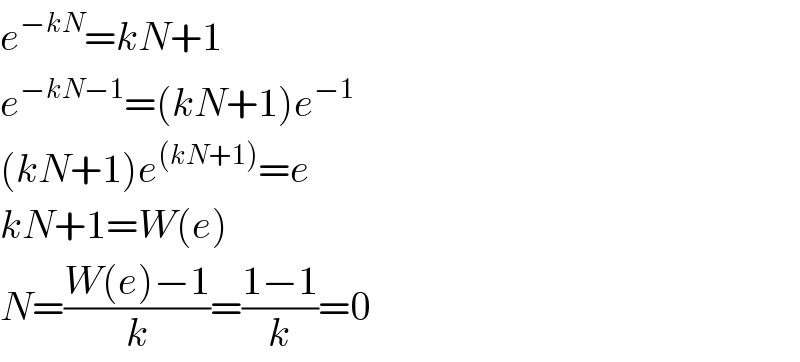
$${e}^{−{kN}} ={kN}+\mathrm{1} \\ $$$${e}^{−{kN}−\mathrm{1}} =\left({kN}+\mathrm{1}\right){e}^{−\mathrm{1}} \\ $$$$\left({kN}+\mathrm{1}\right){e}^{\left({kN}+\mathrm{1}\right)} ={e} \\ $$$${kN}+\mathrm{1}={W}\left({e}\right) \\ $$$${N}=\frac{{W}\left({e}\right)−\mathrm{1}}{{k}}=\frac{\mathrm{1}−\mathrm{1}}{{k}}=\mathrm{0} \\ $$
Commented by tawa tawa last updated on 20/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
