Question Number 96342 by Ar Brandon last updated on 31/May/20

$$\int\mathfrak{e}^{\mathfrak{sin}\left(\mathfrak{x}\right)} \boldsymbol{\mathrm{d}}\mathfrak{x} \\ $$
Commented by prakash jain last updated on 31/May/20
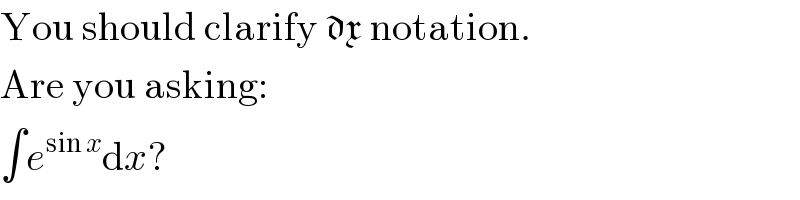
$$\mathrm{You}\:\mathrm{should}\:\mathrm{clarify}\:\mathfrak{dx}\:\mathrm{notation}. \\ $$$$\mathrm{Are}\:\mathrm{you}\:\mathrm{asking}: \\ $$$$\int{e}^{\mathrm{sin}\:{x}} \mathrm{d}{x}? \\ $$
Commented by Ar Brandon last updated on 31/May/20
OK
Answered by mr W last updated on 31/May/20
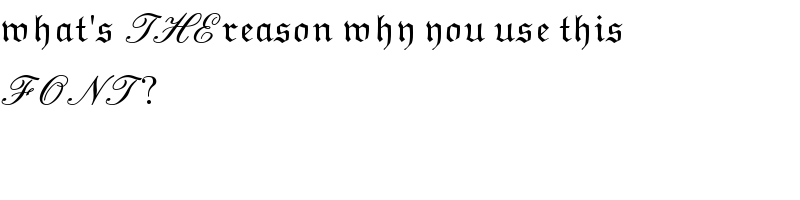
$$\mathfrak{what}'\mathfrak{s}\:\mathscr{THE}\:\mathfrak{reason}\:\mathfrak{why}\:\mathfrak{you}\:\mathfrak{use}\:\mathfrak{this} \\ $$$$\mathscr{FONT}\:? \\ $$
Commented by Ar Brandon last updated on 31/May/20
I just felt like doing so today. Any problem with that ? What's your opinion ?��
Commented by prakash jain last updated on 31/May/20

$$\mathrm{Mathfrak}\:\mathrm{font}\:\mathrm{have}\:\mathrm{special} \\ $$$$\mathrm{meaning}\:\mathrm{in}\:\mathrm{algebra}.\:\mathrm{So}\:\mathrm{better} \\ $$$$\mathrm{to}\:\mathrm{follow}\:\mathrm{convention}\:\mathrm{especially} \\ $$$$\mathrm{when}\:\mathrm{typing}\:\mathrm{math}. \\ $$
Commented by mr W last updated on 01/Jun/20

$${it}'{s}\:{makes}\:{the}\:{reading}\:{unnecessarly} \\ $$$${hard}\:{for}\:{other}\:{people}. \\ $$
Commented by Ar Brandon last updated on 01/Jun/20
Okay, thanks for your opinions. I'll make sure I use the usual font hencefort.��
Answered by M±th+et+s last updated on 31/May/20
![I=∫e^(sin(x)) dx e^u =Σ_(n=0) ^∞ (u^n /(n! )) , u=sin(x) ⇒e^(sin(x)) =Σ_(n=0) ^∞ (((sin(x))^n )/(n!)) I=∫e^(sin(x)) dx=∫Σ_(n=0) ^∞ (((sin(x))^n )/(n!))dx=Σ_(n=0) ^∞ (1/(n!))∫(sin(x))^n dx A=∫(sin(x))^n dx=−cos(x)∗(sin(x))^(n+1) ∗[(sin(x))^2 ]^(((−n)/2)−(1/2)) 2F1[(1/2),((1−n)/2);(3/2);(cos(x))^2 ]+c I=∫e^(sin(x)) dx=−Σ_(n=0) ^∞ (1/(n!))[A]+c notice\ 2F1 is special function called hyper geometric function](https://www.tinkutara.com/question/Q96357.png)
$${I}=\int{e}^{{sin}\left({x}\right)} {dx} \\ $$$${e}^{{u}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{n}} }{{n}!\:}\:,\:{u}={sin}\left({x}\right)\:\Rightarrow{e}^{{sin}\left({x}\right)} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({sin}\left({x}\right)\right)^{{n}} }{{n}!} \\ $$$${I}=\int{e}^{{sin}\left({x}\right)} {dx}=\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({sin}\left({x}\right)\right)^{{n}} }{{n}!}{dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int\left({sin}\left({x}\right)\right)^{{n}} {dx} \\ $$$${A}=\int\left({sin}\left({x}\right)\right)^{{n}} {dx}=−{cos}\left({x}\right)\ast\left({sin}\left({x}\right)\right)^{{n}+\mathrm{1}} \ast\left[\left({sin}\left({x}\right)\right)^{\mathrm{2}} \right]^{\frac{−{n}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}{F}\mathrm{1}\left[\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}−{n}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};\left({cos}\left({x}\right)\right)^{\mathrm{2}} \right]+{c} \\ $$$${I}=\int{e}^{{sin}\left({x}\right)} {dx}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\left[{A}\right]+{c} \\ $$$${notice}\backslash\:\mathrm{2}{F}\mathrm{1}\:{is}\:{special}\:{function}\:{called}\: \\ $$$${hyper}\:{geometric}\:{function} \\ $$
Commented by Ar Brandon last updated on 31/May/20
Thanks
Commented by M±th+et+s last updated on 31/May/20

$${you}\:{are}\:{welcome} \\ $$
Commented by selea last updated on 01/Jun/20
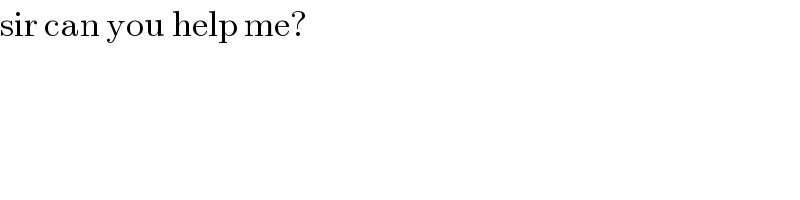
$$\mathrm{sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me}? \\ $$
Commented by M±th+et+s last updated on 01/Jun/20
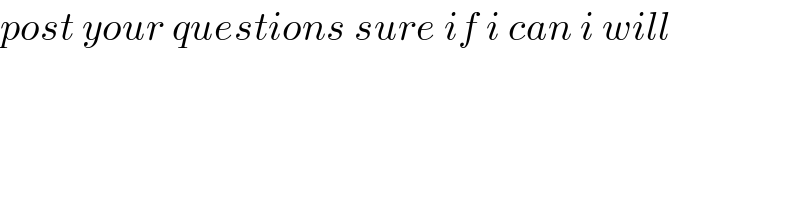
$${post}\:{your}\:{questions}\:{sure}\:{if}\:{i}\:{can}\:{i}\:{will} \\ $$
