Question Number 44695 by manish00@gmail.com last updated on 03/Oct/18
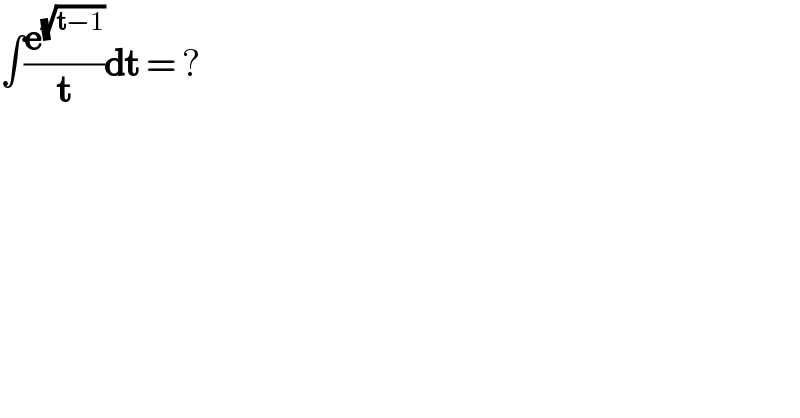
$$\int\frac{\boldsymbol{\mathrm{e}}^{\sqrt{\boldsymbol{\mathrm{t}}−\mathrm{1}}} }{\boldsymbol{\mathrm{t}}}\boldsymbol{\mathrm{dt}}\:=\:? \\ $$
Commented by maxmathsup by imad last updated on 04/Oct/18
![changement (√(t−1))=x give t−1=x^2 ⇒ ∫ (e^(√(t−1)) /t)dt = ∫ (e^x /(1+x^2 )) (2x)dx = ∫ ((2x e^x )/(1+x^2 ))dx by parts u^′ =((2x)/(1+x^2 )) and v=e^x I = e^x ln(1+x^2 ) −∫ e^x ln(1+x^2 ) dx but ∫ e^x ln(1+x^2 )dx = ∫ (Σ_(n=0) ^∞ (x^n /(n!)))ln(1+x^2 )dx =Σ_(n=0) ^∞ (1/(n!)) ∫ x^n ln(1+x^2 )dx =Σ_(n=0) ^∞ (A_n /(n!)) with A_n =∫ x^n ln(1+x^2 )dx by parts A_n = (1/(n+1)) x^(n+1) ln(1+x^2 )−∫ (1/(n+1))x^(n+1) ((2x)/(1+x^2 ))dx =(x^(n+1) /(n+1))ln(1+x^2 ) −(2/(n+1)) ∫ (x^(n+1) /(1+x^2 ))dx...be continued any waythe integal ∫ e^x ln(1+x^2 )dx is alculable on [0,1]....](https://www.tinkutara.com/question/Q44771.png)
$${changement}\:\sqrt{{t}−\mathrm{1}}={x}\:{give}\:{t}−\mathrm{1}={x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\int\:\frac{{e}^{\sqrt{{t}−\mathrm{1}}} }{{t}}{dt}\:=\:\int\:\:\frac{{e}^{{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\left(\mathrm{2}{x}\right){dx}\:=\:\:\int\:\:\frac{\mathrm{2}{x}\:{e}^{{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:{by}\:{parts}\:\:{u}^{'} \:=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{and}\:{v}={e}^{{x}} \\ $$$${I}\:=\:{e}^{{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:−\int\:\:{e}^{{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:{dx}\:\:\:{but} \\ $$$$\int\:\:\:{e}^{{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=\:\int\:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} }{{n}!}\right){ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\:\int\:\:{x}^{{n}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{A}_{{n}} }{{n}!}\:{with}\:{A}_{{n}} =\int\:{x}^{{n}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${by}\:{parts}\:{A}_{{n}} =\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\int\:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:−\frac{\mathrm{2}}{{n}+\mathrm{1}}\:\int\:\:\frac{{x}^{{n}+\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}…{be}\:{continued}\:\:{any}\:{waythe}\:{integal} \\ $$$$\int\:\:{e}^{{x}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:{is}\:{alculable}\:{on}\:\left[\mathrm{0},\mathrm{1}\right]…. \\ $$
Commented by arvinddayama01@gmail.com last updated on 04/Oct/18

$$\mathrm{wrong} \\ $$
