e-tan-sec-sin-d-

Question Number 36459 by rahul 19 last updated on 02/Jun/18

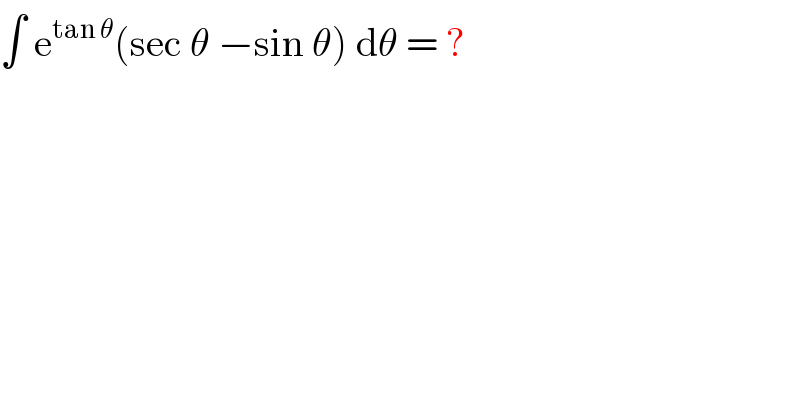
$$\int\:\mathrm{e}^{\mathrm{tan}\:\theta} \left(\mathrm{sec}\:\theta\:−\mathrm{sin}\:\theta\right)\:\mathrm{d}\theta\:=\:? \\ $$

Answered by ajfour last updated on 02/Jun/18

let tan θ=t ⇒ I=∫e^t (sec θ−sin θ)cos^2 θdt =∫e^t (cos θ−((sin θ)/(1+tan^2 θ)))dt =∫e^t ((1/( (√(1+t^2 ))))−(t/((1+t^2 )^(3/2) )))dt =∫e^t [(1/( (√(1+t^2 ))))+(d/dt)((1/( (√(1+t^2 )))))]dt = (e^t /( (√(1+t^2 ))))+c I = e^(tan θ) cos θ +c .

$${let}\:\mathrm{tan}\:\theta={t} \\ $$$$\Rightarrow\:{I}=\int{e}^{{t}} \left(\mathrm{sec}\:\theta−\mathrm{sin}\:\theta\right)\mathrm{cos}\:^{\mathrm{2}} \theta{dt} \\ $$$$\:\:\:\:\:\:\:\:=\int{e}^{{t}} \left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}\right){dt} \\ $$$$\:\:\:\:\:\:\:=\int{e}^{{t}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}−\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\right){dt} \\ $$$$\:\:\:\:\:\:=\int{e}^{{t}} \left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}+\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right)\right]{dt} \\ $$$$\:\:\:\:\:\:=\:\frac{{e}^{{t}} }{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}+{c} \\ $$$$\:\:\:\:\:{I}\:=\:{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta\:+{c}\:. \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Thank you sir ��

Answered by MJS last updated on 02/Jun/18

lol, tricky... ∫e^(tan θ) (sec θ−sin θ)dθ= =∫e^(tan θ) sec θ dθ−∫e^(tan θ) sin θ dθ= [((f′=sin θ ⇒ f=−cos θ)),((g=e^(tan θ) ⇒ g′=e^(tan θ) sec^2 θ)),((∫f′g=fg−∫fg′)) ] =∫e^(tan θ) sec θ dθ+e^(tan θ) cos θ−∫e^(tan θ) cos θ sec^2 θ dθ= =e^(tan θ) cos θ +C

$$\mathrm{lol},\:\mathrm{tricky}… \\ $$$$\int\mathrm{e}^{\mathrm{tan}\:\theta} \left(\mathrm{sec}\:\theta−\mathrm{sin}\:\theta\right){d}\theta= \\ $$$$=\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sec}\:\theta\:{d}\theta−\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sin}\:\theta\:{d}\theta= \\ $$$$\:\:\:\:\:\begin{bmatrix}{{f}'=\mathrm{sin}\:\theta\:\Rightarrow\:{f}=−\mathrm{cos}\:\theta}\\{{g}=\mathrm{e}^{\mathrm{tan}\:\theta} \:\Rightarrow\:{g}'=\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sec}^{\mathrm{2}} \:\theta}\\{\int{f}'{g}={fg}−\int{fg}'}\end{bmatrix} \\ $$$$=\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sec}\:\theta\:{d}\theta+\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta−\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta\:\mathrm{sec}^{\mathrm{2}} \:\theta\:{d}\theta= \\ $$$$=\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta\:+{C} \\ $$

Commented by rahul 19 last updated on 02/Jun/18

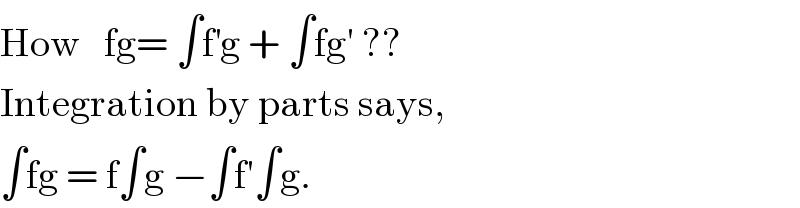
How fg= ∫f^′ g + ∫fg′ ?? Integration by parts says, ∫fg = f∫g −∫f′∫g.

$$\mathrm{How}\:\:\:\mathrm{fg}=\:\int\mathrm{f}^{'} \mathrm{g}\:+\:\int\mathrm{fg}'\:?? \\ $$$$\mathrm{Integration}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{says}, \\ $$$$\int\mathrm{fg}\:=\:\mathrm{f}\int\mathrm{g}\:−\int\mathrm{f}'\int\mathrm{g}. \\ $$

Commented by MJS last updated on 02/Jun/18

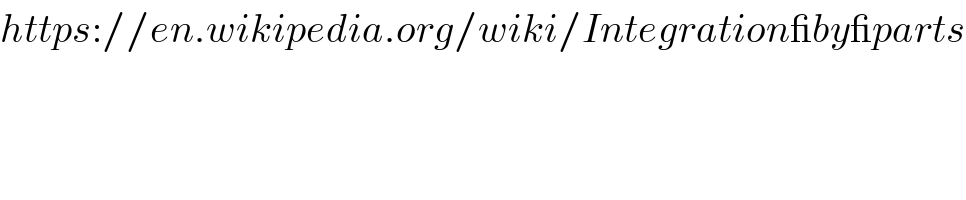
$${https}://{en}.{wikipedia}.{org}/{wiki}/{Integration\_by\_parts} \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Sir if you want to integrate say ∫xsin x then g=sin x , f=x . (ILATE ) ⇒ ∫g= −cos x , f′ = 1. ∫fg= f∫g − ∫f′ ∫g ⇒ x(−cos x) − ∫−(cos x) ⇒ −xcos x+sin x+c.

$$\mathrm{Sir}\:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{integrate}\:\mathrm{say} \\ $$$$\int{x}\mathrm{sin}\:{x}\:\mathrm{then}\:\mathrm{g}=\mathrm{sin}\:{x}\:,\:\mathrm{f}={x}\:.\:\left(\mathrm{ILATE}\:\right) \\ $$$$\Rightarrow\:\int\mathrm{g}=\:−\mathrm{cos}\:{x}\:,\:\mathrm{f}'\:=\:\mathrm{1}. \\ $$$$\int\mathrm{fg}=\:\mathrm{f}\int\mathrm{g}\:−\:\int\mathrm{f}'\:\int\mathrm{g} \\ $$$$\:\Rightarrow\:{x}\left(−\mathrm{cos}\:{x}\right)\:−\:\int−\left(\mathrm{cos}\:{x}\right) \\ $$$$\Rightarrow\:−{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+{c}. \\ $$

Commented by MJS last updated on 02/Jun/18

we come from differentation: (uv)′=u′v+uv′ now integrate both sides: uv=∫u′v+∫uv′ that′s how I learned it...

$$\mathrm{we}\:\mathrm{come}\:\mathrm{from}\:\mathrm{differentation}: \\ $$$$\left({uv}\right)'={u}'{v}+{uv}' \\ $$$$\mathrm{now}\:\mathrm{integrate}\:\mathrm{both}\:\mathrm{sides}: \\ $$$${uv}=\int{u}'{v}+\int{uv}' \\ $$$$\mathrm{that}'\mathrm{s}\:\mathrm{how}\:\mathrm{I}\:\mathrm{learned}\:\mathrm{it}… \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Is this also called integration by parts? Anyways,thanks!!

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{also}\:\mathrm{called}\:\mathrm{integration}\:\mathrm{by}\:\mathrm{parts}? \\ $$$$\mathrm{Anyways},\mathrm{thanks}!! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply