Question Number 24828 by moxhix last updated on 27/Nov/17

$$\int\sqrt{{e}^{{x}} +\mathrm{1}}{dx}=? \\ $$
Commented by mrW1 last updated on 27/Nov/17

$${see}\:{Q}\mathrm{24670} \\ $$
Commented by moxhix last updated on 27/Nov/17

$${Thank}\:{you} \\ $$
Commented by maxmathsup by imad last updated on 24/May/19
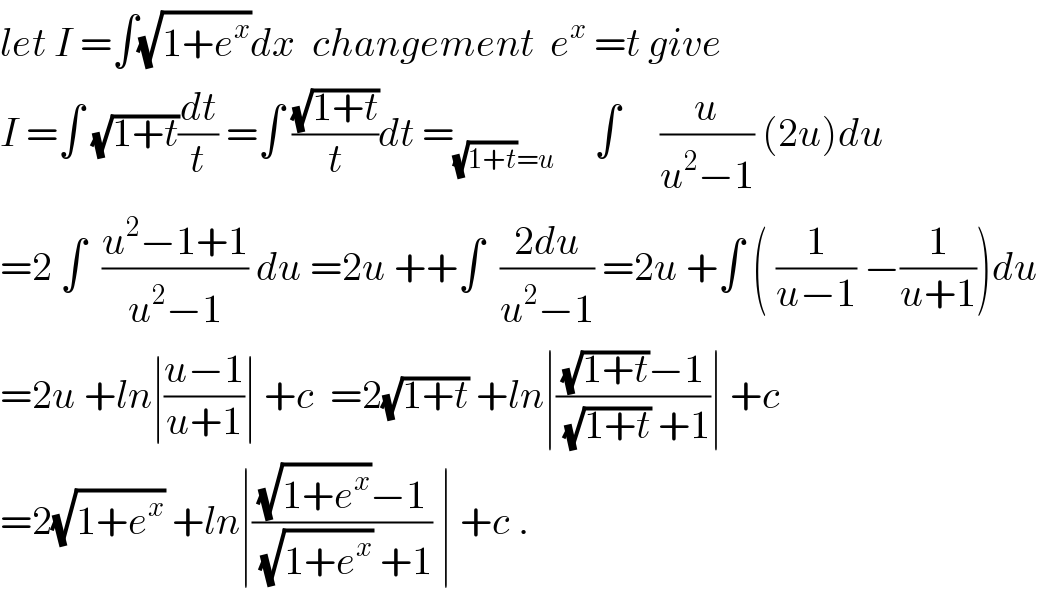
$${let}\:{I}\:=\int\sqrt{\mathrm{1}+{e}^{{x}} }{dx}\:\:{changement}\:\:{e}^{{x}} \:={t}\:{give} \\ $$$${I}\:=\int\:\sqrt{\mathrm{1}+{t}}\frac{{dt}}{{t}}\:=\int\:\frac{\sqrt{\mathrm{1}+{t}}}{{t}}{dt}\:=_{\sqrt{\mathrm{1}+{t}}={u}} \:\:\:\:\:\int\:\:\:\:\:\frac{{u}}{{u}^{\mathrm{2}} −\mathrm{1}}\:\left(\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{2}\:\int\:\:\frac{{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}\:{du}\:=\mathrm{2}{u}\:++\int\:\:\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{2}{u}\:+\int\:\left(\:\frac{\mathrm{1}}{{u}−\mathrm{1}}\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du} \\ $$$$=\mathrm{2}{u}\:+{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\:+{c}\:\:=\mathrm{2}\sqrt{\mathrm{1}+{t}}\:+{ln}\mid\frac{\sqrt{\mathrm{1}+{t}}−\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}}\:+\mathrm{1}}\mid\:+{c} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}+{e}^{{x}} }\:+{ln}\mid\frac{\sqrt{\mathrm{1}+{e}^{{x}} }−\mathrm{1}}{\:\sqrt{\mathrm{1}+{e}^{{x}} }\:+\mathrm{1}}\:\mid\:+{c}\:. \\ $$
Answered by Eng.Firas last updated on 27/Nov/17

$${let}\:{e}^{{x}} ={tan}^{\mathrm{2}} \theta \\ $$$$\:{e}^{{x}} {dx}=\mathrm{2}{tan}\theta\:{sec}^{\mathrm{2}} \theta\:{d}\theta \\ $$$${dx}=\mathrm{2}\frac{{sec}^{\mathrm{2}} \theta}{{tan}\theta}\:{d}\theta \\ $$$$\int\sqrt{{tan}^{\mathrm{2}} \theta+\mathrm{1}\:}\frac{{sec}^{\mathrm{2}} \theta}{{tan}\theta}{d}\theta \\ $$$$\int{sec}\theta\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{{tan}\theta}{d}\theta \\ $$$$\int{sec}\theta\:{cot}\theta\:{d}\theta\:+\int{sec}\theta\:{tan}\theta\:{d}\theta \\ $$$$\int\:{csc}\theta\:{d}\theta\:+\int{sec}\theta\:{tan}\theta\:{d}\theta \\ $$$$=−{ln}\mid{csc}\theta+{cot}\theta\mid+{sec}\theta+{C} \\ $$$$=−{ln}\mid\frac{\sqrt{\mathrm{1}+{e}^{{x}} }}{\:\sqrt{{e}^{{x}} }}+\frac{\mathrm{1}}{\:\sqrt{{e}^{{x}} }}\mid+\sqrt{{e}^{{x}} +\mathrm{1}}+{C} \\ $$$$ \\ $$$$ \\ $$
Commented by moxhix last updated on 27/Nov/17

$${Thank}\:{you} \\ $$
