Question Number 95115 by bobhans last updated on 23/May/20
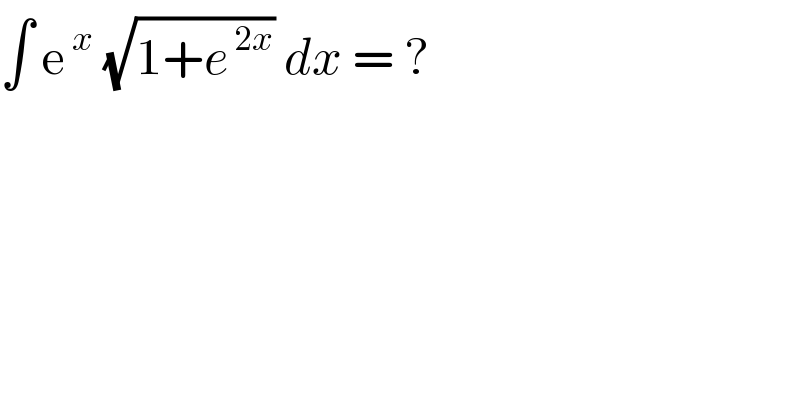
$$\int\:\mathrm{e}^{\:{x}} \:\sqrt{\mathrm{1}+{e}^{\:\mathrm{2}{x}} }\:{dx}\:=\:?\: \\ $$
Answered by i jagooll last updated on 23/May/20
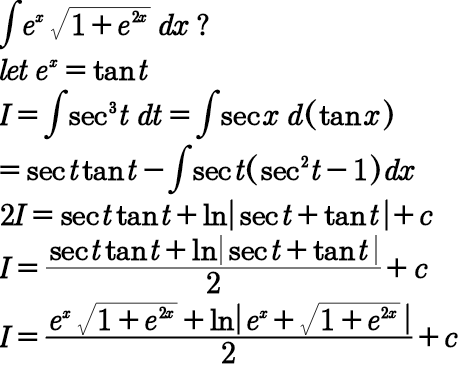
Commented by bobhans last updated on 23/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by peter frank last updated on 23/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mathmax by abdo last updated on 23/May/20

$$\mathrm{I}\:=\int\:\mathrm{e}^{\mathrm{x}} \sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\mathrm{dx}\:\:\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{1}+\mathrm{e}^{\mathrm{2x}} =\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{e}^{\mathrm{2x}} =\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow\mathrm{dx}\:=\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}×\mathrm{t}\:×\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:=\int\:\:\frac{\mathrm{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dt} \\ $$$$=\int\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dt}\:=\int\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:+\int\:\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\mathrm{changement}\:\mathrm{t}\:=\mathrm{chu}\:\mathrm{give}\: \\ $$$$\int\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:=\int\mathrm{sh}^{\mathrm{2}} \mathrm{u}\:\mathrm{du}\:=\int\:\frac{\mathrm{ch}\left(\mathrm{2u}\right)−\mathrm{1}}{\mathrm{2}}\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh}\left(\mathrm{2u}\right)−\frac{\mathrm{u}}{\mathrm{2}}\:+\mathrm{c}_{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\left(\mathrm{u}\right)\mathrm{chu}−\frac{\mathrm{u}}{\mathrm{2}}+\mathrm{c}_{\mathrm{0}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\right)+\mathrm{c}_{\mathrm{0}} \\ $$$$\int\:\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}\:=_{\mathrm{t}=\mathrm{chu}} \:\:\:\:\int\:\:\:\frac{\mathrm{shu}}{\mathrm{shu}}\mathrm{du}\:=\mathrm{u}\:+\mathrm{c}_{\mathrm{1}} =\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\right)\:+\mathrm{c}_{\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{t}\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\right)+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }×\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\:+\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} −\mathrm{1}}\right)\:+\mathrm{C} \\ $$$$=\frac{\mathrm{e}^{\mathrm{x}} \sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\right)\:+\mathrm{C} \\ $$
