Question Number 96083 by john santu last updated on 29/May/20
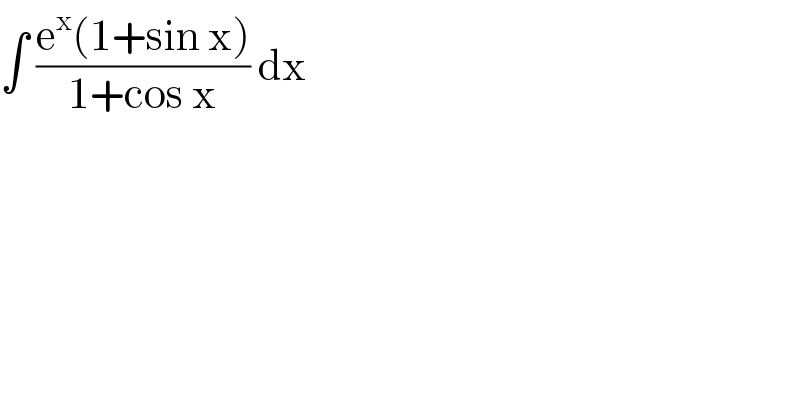
$$\int\:\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\: \\ $$
Answered by john santu last updated on 29/May/20
![∫ ((e^x /(1+cos x)) + ((e^x sin x)/(1+cos x)))dx = ∫ [ (e^x /(2cos^2 ((x/2)))) + e^x tan ((x/2)) ] dx = ∫ [(1/2)e^x sec^2 ((x/2)) +e^x tan ((x/2))] dx = ∫ d (e^x tan ((x/2))) = e^x tan ((x/2)) + c](https://www.tinkutara.com/question/Q96084.png)
$$\int\:\left(\frac{{e}^{{x}} }{\mathrm{1}+\mathrm{cos}\:{x}}\:+\:\frac{{e}^{{x}} \mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}\right){dx}\:=\: \\ $$$$\int\:\left[\:\frac{{e}^{{x}} }{\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\:+\:{e}^{{x}} \:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\:\right]\:{dx}\:= \\ $$$$\int\:\left[\frac{\mathrm{1}}{\mathrm{2}}{e}^{{x}} \mathrm{sec}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:+{e}^{{x}} \:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\right]\:{dx}\:= \\ $$$$\int\:{d}\:\left({e}^{{x}} \mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\right)\:=\:{e}^{{x}} \:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\:+\:{c}\: \\ $$
