Question Number 151278 by mathdanisur last updated on 19/Aug/21
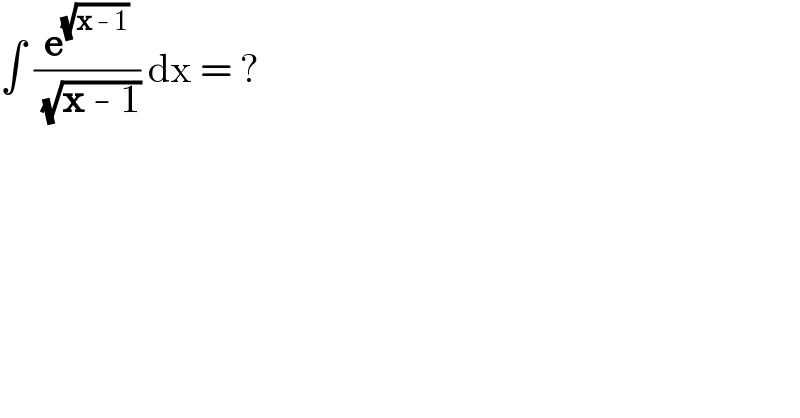
$$\int\:\frac{\boldsymbol{\mathrm{e}}^{\sqrt{\boldsymbol{\mathrm{x}}\:-\:\mathrm{1}}} }{\:\sqrt{\boldsymbol{\mathrm{x}}\:-\:\mathrm{1}}}\:\mathrm{dx}\:=\:? \\ $$
Answered by Ar Brandon last updated on 19/Aug/21

$$\mathrm{I}=\int\frac{{e}^{\sqrt{{x}−\mathrm{1}}} }{\:\sqrt{{x}−\mathrm{1}}}{dx},\:{u}=\sqrt{{x}−\mathrm{1}}\Rightarrow{du}=\frac{{dx}}{\mathrm{2}\sqrt{{x}−\mathrm{1}}} \\ $$$$\:\:=\mathrm{2}\int{e}^{{u}} {du}=\mathrm{2}{e}^{{u}} +{C}=\mathrm{2}{e}^{\sqrt{{x}−\mathrm{1}}} +{C} \\ $$
Commented by mathdanisur last updated on 19/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
