Question Number 56060 by necx1 last updated on 09/Mar/19
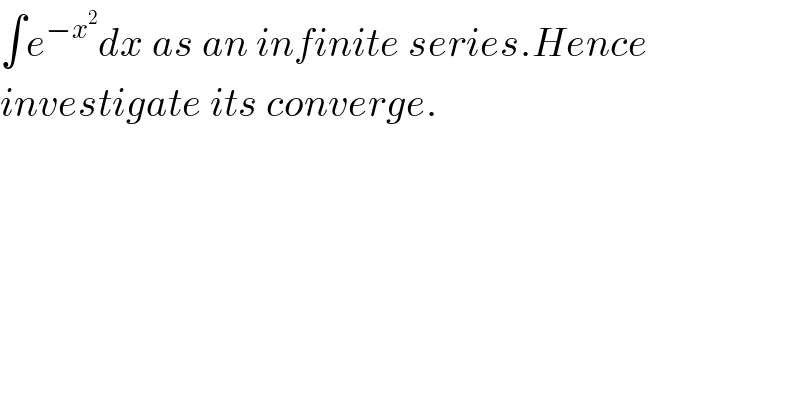
$$\int{e}^{−{x}^{\mathrm{2}} } {dx}\:{as}\:{an}\:{infinite}\:{series}.{Hence} \\ $$$${investigate}\:{its}\:{converge}. \\ $$
Commented by maxmathsup by imad last updated on 09/Mar/19
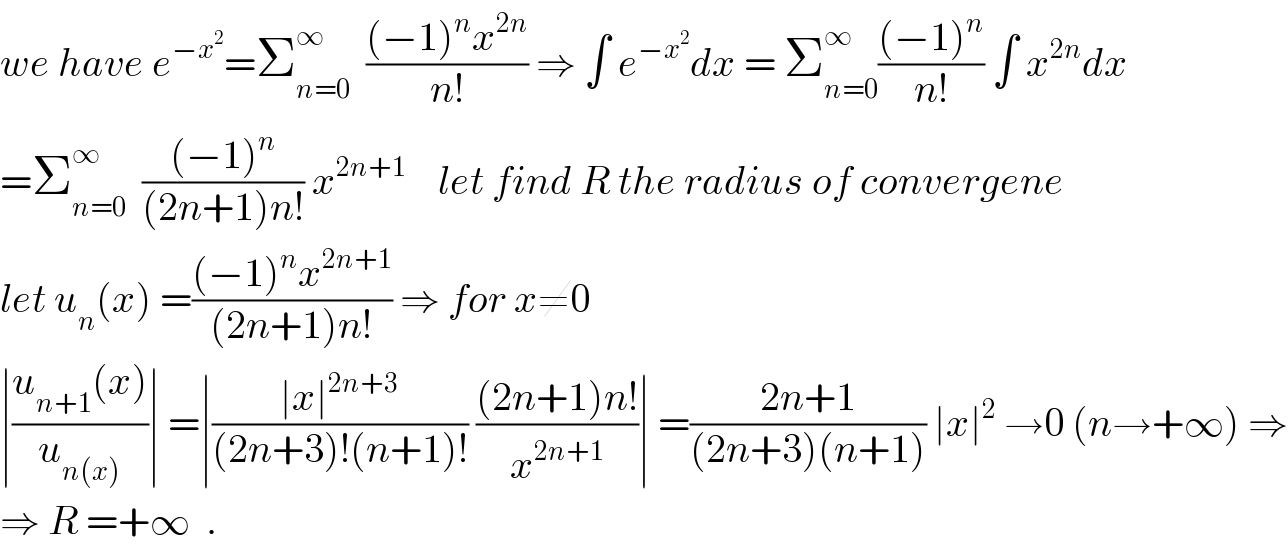
$${we}\:{have}\:{e}^{−{x}^{\mathrm{2}} } =\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!}\:\Rightarrow\:\int\:{e}^{−{x}^{\mathrm{2}} } {dx}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:\int\:{x}^{\mathrm{2}{n}} {dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:\:\:{let}\:{find}\:{R}\:{the}\:{radius}\:{of}\:{convergene} \\ $$$${let}\:{u}_{{n}} \left({x}\right)\:=\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\:\Rightarrow\:{for}\:{x}\neq\mathrm{0}\: \\ $$$$\mid\frac{{u}_{{n}+\mathrm{1}} \left({x}\right)}{{u}_{{n}\left({x}\right)} }\mid\:=\mid\frac{\mid{x}\mid^{\mathrm{2}{n}+\mathrm{3}} }{\left(\mathrm{2}{n}+\mathrm{3}\right)!\left({n}+\mathrm{1}\right)!}\:\frac{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}{{x}^{\mathrm{2}{n}+\mathrm{1}} }\mid\:=\frac{\mathrm{2}{n}+\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{3}\right)\left({n}+\mathrm{1}\right)}\:\mid{x}\mid^{\mathrm{2}} \:\rightarrow\mathrm{0}\:\left({n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\Rightarrow\:{R}\:=+\infty\:\:. \\ $$
Commented by necx1 last updated on 09/Mar/19

$${Thanks}\:{for}\:{the}\:{help}\:{tho}\:{I}\:{really}\:{do}\:{not} \\ $$$${understand}.\:{Please}\:{shed}\:{more}\:{light} \\ $$
Commented by maxmathsup by imad last updated on 09/Mar/19
$${sir}\:{take}\:{a}\:{look}\:\:{at}\:{cknvergence}\:{of}\:{serie}\:{subject}\:… \\ $$
