Question Number 150967 by EDWIN88 last updated on 17/Aug/21
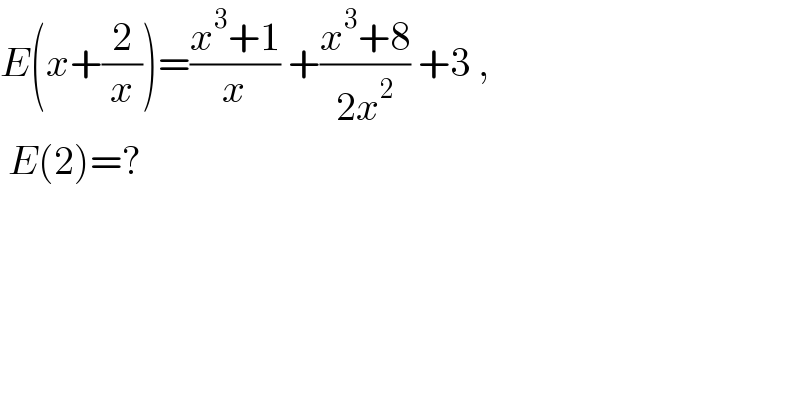
$${E}\left({x}+\frac{\mathrm{2}}{{x}}\right)=\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}}\:+\frac{{x}^{\mathrm{3}} +\mathrm{8}}{\mathrm{2}{x}^{\mathrm{2}} }\:+\mathrm{3}\:, \\ $$$$\:{E}\left(\mathrm{2}\right)=? \\ $$
Answered by john_santu last updated on 17/Aug/21
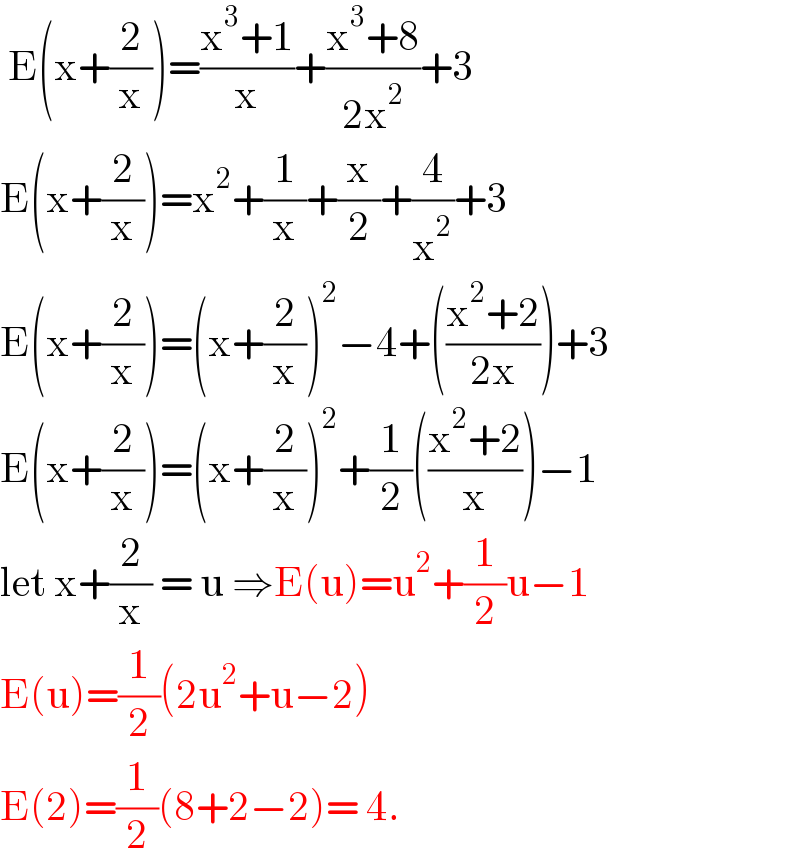
$$\:\mathrm{E}\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)=\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{8}}{\mathrm{2x}^{\mathrm{2}} }+\mathrm{3} \\ $$$$\mathrm{E}\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)=\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{3} \\ $$$$\mathrm{E}\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)=\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{4}+\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2x}}\right)+\mathrm{3} \\ $$$$\mathrm{E}\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)=\left(\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{x}}\right)−\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{x}+\frac{\mathrm{2}}{\mathrm{x}}\:=\:\mathrm{u}\:\Rightarrow\mathrm{E}\left(\mathrm{u}\right)=\mathrm{u}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{u}−\mathrm{1} \\ $$$$\mathrm{E}\left(\mathrm{u}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2u}^{\mathrm{2}} +\mathrm{u}−\mathrm{2}\right) \\ $$$$\mathrm{E}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{8}+\mathrm{2}−\mathrm{2}\right)=\:\mathrm{4}. \\ $$
