Question Number 88089 by ar247 last updated on 08/Apr/20

$$\int\frac{{e}^{{x}} }{{e}^{\mathrm{2}} −\mathrm{9}}{dx} \\ $$
Commented by ar247 last updated on 08/Apr/20

$${help} \\ $$
Answered by Rio Michael last updated on 08/Apr/20
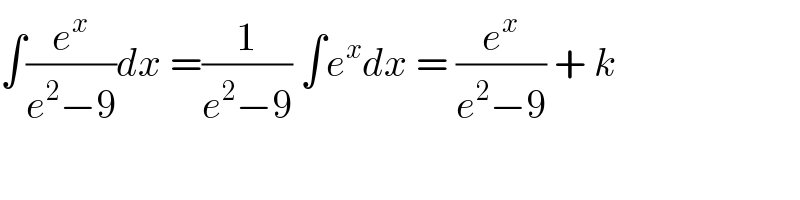
$$\int\frac{{e}^{{x}} }{{e}^{\mathrm{2}} −\mathrm{9}}{dx}\:=\frac{\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{9}}\:\int{e}^{{x}} {dx}\:=\:\frac{{e}^{{x}} }{{e}^{\mathrm{2}} −\mathrm{9}}\:+\:{k}\: \\ $$
