Question Number 156600 by ZiYangLee last updated on 13/Oct/21
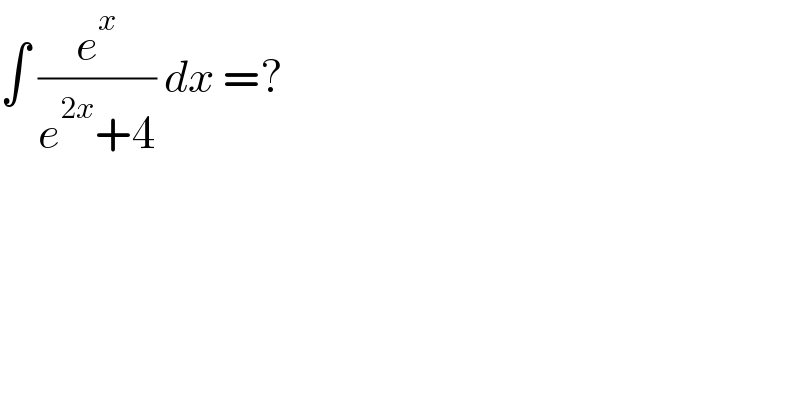
$$\int\:\frac{{e}^{{x}} }{{e}^{\mathrm{2}{x}} +\mathrm{4}}\:{dx}\:=?\: \\ $$
Answered by gsk2684 last updated on 13/Oct/21
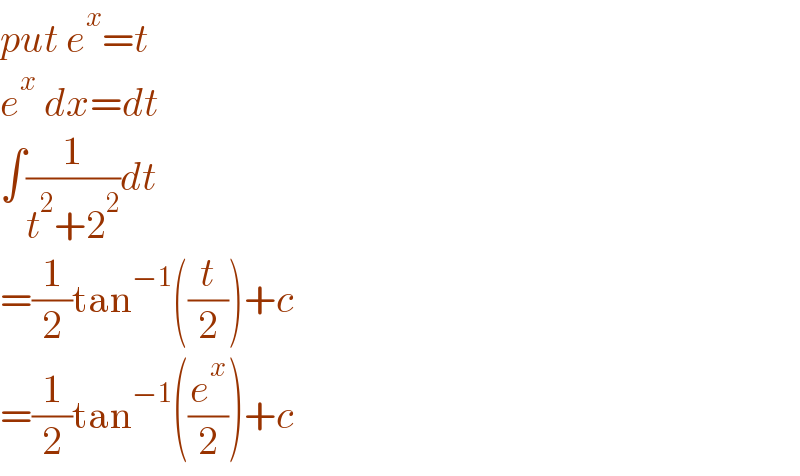
$${put}\:{e}^{{x}} ={t} \\ $$$${e}^{{x}} \:{dx}={dt} \\ $$$$\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{t}}{\mathrm{2}}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{e}^{{x}} }{\mathrm{2}}\right)+{c}\: \\ $$
Answered by physicstutes last updated on 13/Oct/21
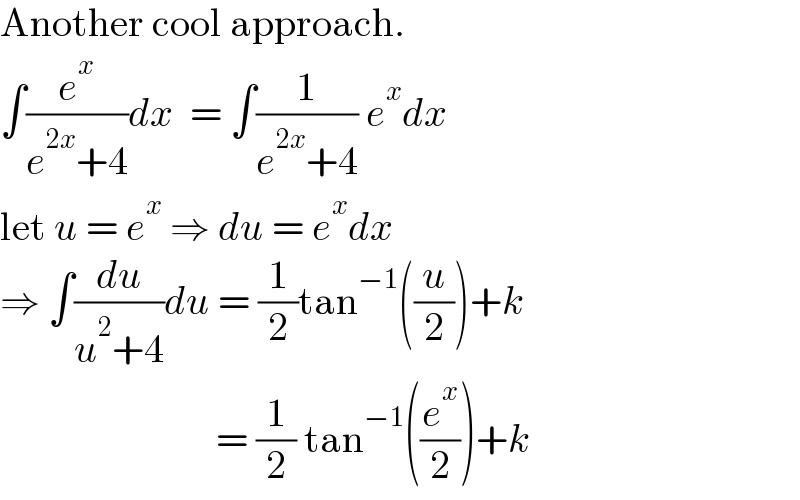
$$\mathrm{Another}\:\mathrm{cool}\:\mathrm{approach}. \\ $$$$\int\frac{{e}^{{x}} }{{e}^{\mathrm{2}{x}} +\mathrm{4}}{dx}\:\:=\:\int\frac{\mathrm{1}}{{e}^{\mathrm{2}{x}} +\mathrm{4}}\:{e}^{{x}} {dx} \\ $$$$\mathrm{let}\:{u}\:=\:{e}^{{x}} \:\Rightarrow\:{du}\:=\:{e}^{{x}} {dx} \\ $$$$\Rightarrow\:\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{4}}{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{u}}{\mathrm{2}}\right)+{k} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{e}^{{x}} }{\mathrm{2}}\right)+{k} \\ $$
